9 月 2016 | 第2页共4页 | David 9的博客 --- 不怕"过拟合"

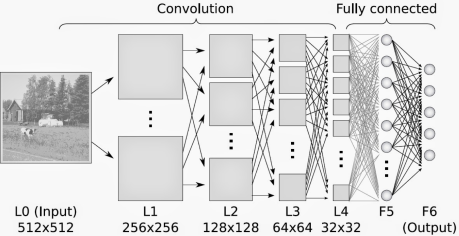
Pycon 2016 tensorflow 研讨会总结 — tensorflow 手把手入门, 用”人话”解释CNN #第三讲 CNN

首先什么是CNN? 其实, 用”人话”简洁地说, 卷积神经网络关键就在于”卷积”二字, 卷积是指神经网络对输入的特征提取的方法不同. 学过卷积的同学一定知道, 在通信中, 卷积是对输入信号经过持续的转换, 持续输出另一组信号的过程.

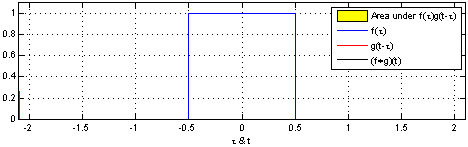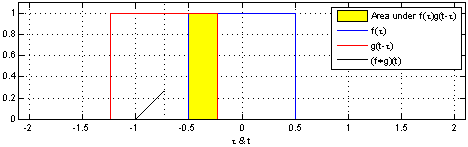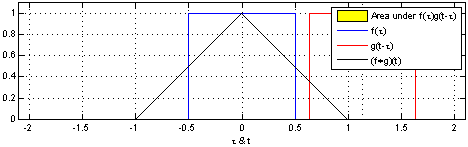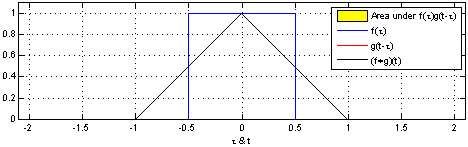
上图来自维基百科, 经过红色方框的持续转换, 我们关注红色方框和蓝色方框的重叠面积, 于是我们得到新的输出: 黑色线的函数. 这正是通过卷积生成新函数的过程. 继续阅读Pycon 2016 tensorflow 研讨会总结 — tensorflow 手把手入门, 用”人话”解释CNN #第三讲 CNN

在第3期 “#3 集成学习–机器学习中的群策群力” 中我们谈到, 集成学习是使用一系列学习器进行学习，以某种规则把各个学习结果进行整合，从而获得比基学习器有更好学习效果的集成学习器.

集成学习之所以有更好的学习效果, 与单个基学习器的“多样性”或者说“差异性”密不可分.

正像大自然万物的多样性随处可见, 生物繁衍产生下一代的过程.

集成学习的关键是允许每个单个学习器有各自的差异性, 同时又有一定错误率上界的情况下, 集成所有单个学习器. 正如在繁衍下一代时, 父母各自贡献自己的DNA片段, 取长补短, 去重组得到新的下一代基因组合.

对此, [Krogh and Vedelsby, 1995]给出了一个称之为”误差-分歧分解“(error-ambiguity decomposition)的漂亮式子:

$E =\overline{E} - \overline{A}$

$E$ 表示集成后模型的泛化误差. 继续阅读聊聊集成学习和”多样性”, “差异性”的那些事儿~

今天拜读南大周志华老师今年1月的新书《机器学习》, 决定趴一趴Logistic Regression. 在各种书籍, 网络中它们翻译各不相同, 有叫”逻辑回归”的, 也有叫”对数回归” “的, 也有叫”对数几率回归”. 其实, 这几个概念都是同一个概念.

当然, 我是认为周志华老师的”对数几率回归”的说法比较恰当.

那David 9我就来当个”传教士”, 说说什么是”对数几率回归”, 为什么要叫”对数几率回归” ?

说”对数几率回归”, 我们必须从”线性回归”和”广义线性回归”说起:

线性回归非常简单, 给你一个样本集合 $D = {(x_1, y_1), (x_2, y_2), (x_3, y_3), (x_i, y_i)......(x_m, y_m)}$ , 注意这里 $x_i, y_i$ 可以都是高维向量

于是目标是找到一个好的线性模拟:

$f(x_i) = wx_i + b$

求出w, b, 这个模型就算固定了. 如何衡量样本y和你的f(x)之间的差别, 每个人都有不同的方法, 最常用的, 当然是最小二乘法, 也就是用欧氏距离去衡量.

Whatever ~ 我们用一条线去模拟和预测未来的数据, 即, 给我一个x值, 我能给你一个预测的y值, 这就是线性回归.

“广义线性回归”又是怎么回事?

也非常简单, 我们不再只是用线性函数模拟数据, 而是在外层加了一个单调可微函数g, 即:

$f(x_i) = g^{-1}(wx_i + b)$

如果g=ln , 则这个广义线性模型就变为对数线性回归. 其实本质就是给原来线性变换加上一个非线性变换(或者说映射), 使得模拟的函数有非线性的属性, 但是, 本质上调参还是线性的, 主体是内部线性的调参. 来一发《机器学习》中的直观截图: