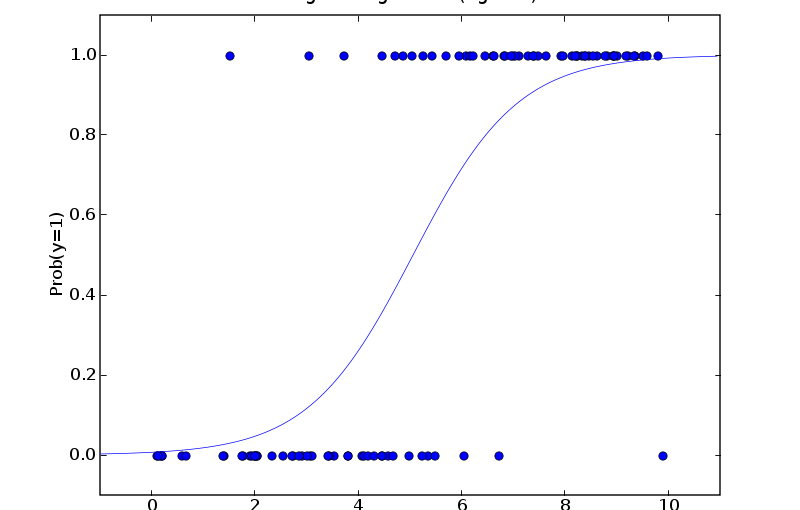
今天拜读南大周志华老师今年1月的新书《机器学习》, 决定趴一趴Logistic Regression. 在各种书籍, 网络中它们翻译各不相同, 有叫”逻辑回归”的, 也有叫”对数回归” “的, 也有叫”对数几率回归”. 其实, 这几个概念都是同一个概念.
当然, 我是认为周志华老师的”对数几率回归”的说法比较恰当.
那David 9我就来当个”传教士”, 说说什么是”对数几率回归”, 为什么要叫”对数几率回归” ?
说”对数几率回归”, 我们必须从”线性回归”和”广义线性回归”说起:
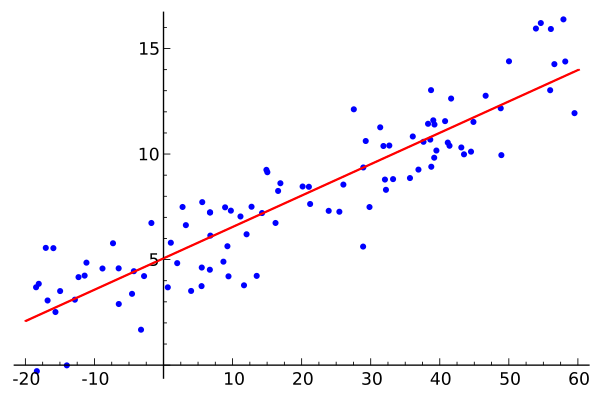
线性回归非常简单, 给你一个样本集合
, 注意这里
可以都是高维向量
于是目标是找到一个好的线性模拟:
求出w, b, 这个模型就算固定了. 如何衡量样本y和你的f(x)之间的差别, 每个人都有不同的方法, 最常用的, 当然是最小二乘法, 也就是用欧氏距离去衡量.
Whatever ~ 我们用一条线去模拟和预测未来的数据, 即, 给我一个x值, 我能给你一个预测的y值, 这就是线性回归.
“广义线性回归”又是怎么回事?
也非常简单, 我们不再只是用线性函数模拟数据, 而是在外层加了一个单调可微函数g, 即:
如果g=ln , 则这个广义线性模型就变为对数线性回归. 其实本质就是给原来线性变换加上一个非线性变换(或者说映射), 使得模拟的函数有非线性的属性, 但是, 本质上调参还是线性的, 主体是内部线性的调参. 来一发《机器学习》中的直观截图:
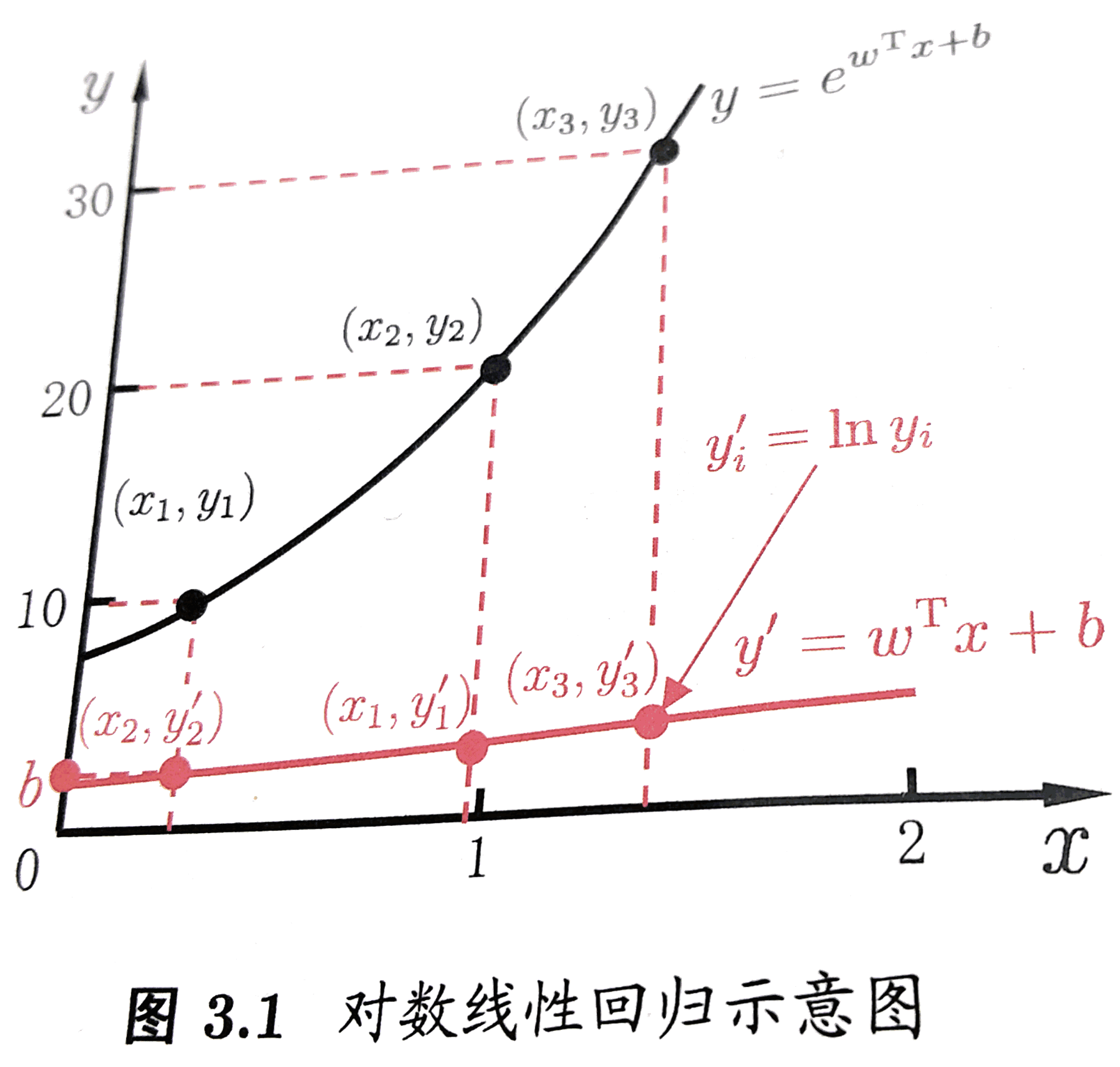继续阅读#8 究竟什么是”逻辑回归”, “对数几率回归”, 和”Logistic Regression”… 知道它们是同一个概念似乎还不够…