曾经的存在主义与结构主义的争论,在量子世界中似乎用概率和大量抽样完成了和解 — David 9
上世纪60年代哲学界有一场关于存在主义与结构主义的争论:存在主义认为一个人的发展是由“自由意识”和欲望主导的; 结构主义认为占主导的其实是社会中的经济、政治、伦理、宗教等结构性因素,人只是巨大结构中的一部分。
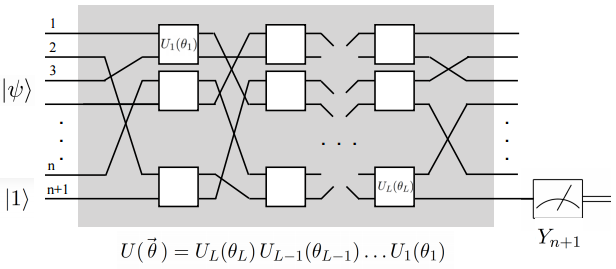
究竟是什么塑造了一个人也许难以确定。而对于量子世界,一个qubit(量子比特)的状态,不仅受到量子系统的磁场影响,qubit本身也有自身状态的变化概率和扰动。我们一会儿可以看到,量子系统的输出,即那个qubit的最终观测状态,是用概率和大量抽样判定的:
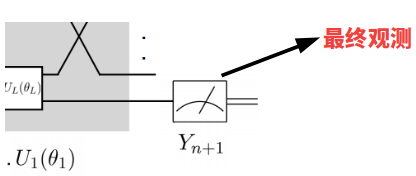
在细讲QNN前(量子神经网络其实是一个量子系统),David 9 有必要介绍一下量子计算本身的一些基础知识 。
首先,量子计算与传统计算机的不同,可从qubit(量子比特)说起,我们知道与电子计算机非“0”即“1”相比,qubit的状态可能同时介于“0”和“1”之间:
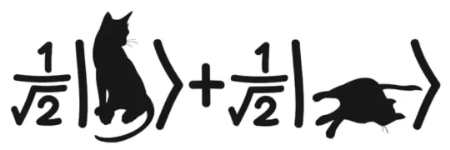
即所谓的“薛定谔的猫”的叠加态(superposition):
![]() (|0>+|1>) (在量子物理中符号|x>表示状态x)
(|0>+|1>) (在量子物理中符号|x>表示状态x)
你们可能会问David,为什么状态系数是 1/![]() ? 这是量子物理中的一个约定(规范化),即平方和等于1:
? 这是量子物理中的一个约定(规范化),即平方和等于1:
α^2+β^2=1
其中α和β就是状态的系数,是不是让你联想到圆形几何 ?
是的,在量子物理中可以把qubit想象成粒子球体(叠加或非叠加态):
三维世界中qubit的自旋状态非常灵活,可以上自旋(|0>),可以下自旋(|1>),可以像地球一样斜着自旋:

当然也可以叠加态自旋(![]() (|0>+|1>) )
(|0>+|1>) )
有了这么多种qubit状态,从根本上导致量子计算的信息量级比传统计算机大的多。
传统的2个bit位的计算机只能编码4种状态:00, 01, 10, 11 ,因为它只有2个位的自由度,所以n个bit位能编码的信息只有2^n (即![]() )
)
而如果一个量子计算机有2个qubit,传统计算机的00, 01, 10, 11这些状态就可以同时出现,这4个状态本身变为4个自由度:
David 9
Latest posts by David 9 (see all)
- 修订特征已经变得切实可行, “特征矫正工程”是否会成为潮流? - 27 3 月, 2024
- 量子计算系列#2 : 量子机器学习与量子深度学习补充资料,QML,QeML,QaML - 29 2 月, 2024
- “现象意识”#2:用白盒的视角研究意识和大脑,会是什么景象?微意识,主体感,超心智,意识中层理论 - 16 2 月, 2024