The knowledge of certain principles easily compensates the lack of knowledge of certain facts. —— Claude Adrien Helvétius
人类的快速脑补能力有时也是缺陷,就像哲学家爱尔维修(Helvétius)说的,人们手里一旦有了“锤子”,眼中一切都会变成“钉子”,如果没办法看做“钉子”,首先会想到的,也是做个更好的锤子作为补偿。
现在,CNN或神经网络就是那个“锤子”,各种数据处理(增强)方法就是那个“钉子”。99%的工作都围绕着如何让一对“锤子““钉子”更好地配合。
而我们今天聚焦的就是一个更好的“大锤子” —— Geometric Deep Learning
ICLR2021上几何深度学习(Geometric Deep Learning)博得了很多眼球,究其根源,其实它是图深度学习(graph deep learning)的延伸甚至等价,而与深度学习的关系并不密切(主讲人Michael Bronstein之前也是专注graph representation的)。
因为其强大的抽象能力,“几何”二字让深度学习这把“锤子”更大了。
首先,这里的几何主要指的是非欧几何(拓扑学流形学)的领域。研究的是极度抽象的概念如:群论中的对称群不变群等变换:
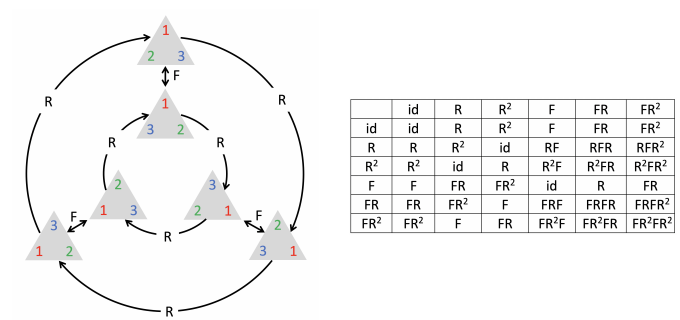

这些对万物实体的极度抽象,帮助我们解决的不仅仅是图像问题,与图论有关的群组问题、化学分子分析,3D测绘等等问题,都可以得到匹配的应用: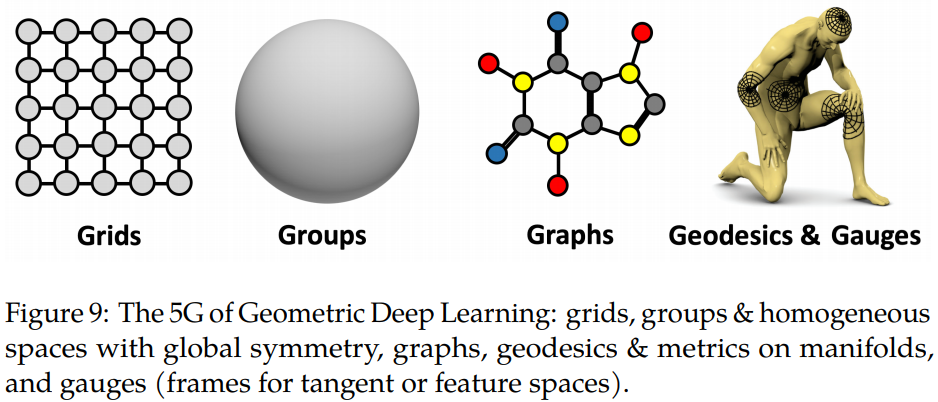
几何深度学习天然自带一些很好的性质(这些性质其实卷积网络中已经经常用到),比如对称的稳定性,视觉上,许多物体其实是同一个物体,只要考虑对称性一切都可以迎刃而解,而传统卷积网络更多地使用数据增强(旋转,平移,翻转)来补偿这一目的,这个我们在胶囊网络中讨论过,

甚至,我们在几何深度学习中,对不变群的范围要放的更宽泛,如在一段视频中,有两辆小车相向而行,无论速度如何,或者有遮挡,视频的语义还是两辆小车相向行驶:
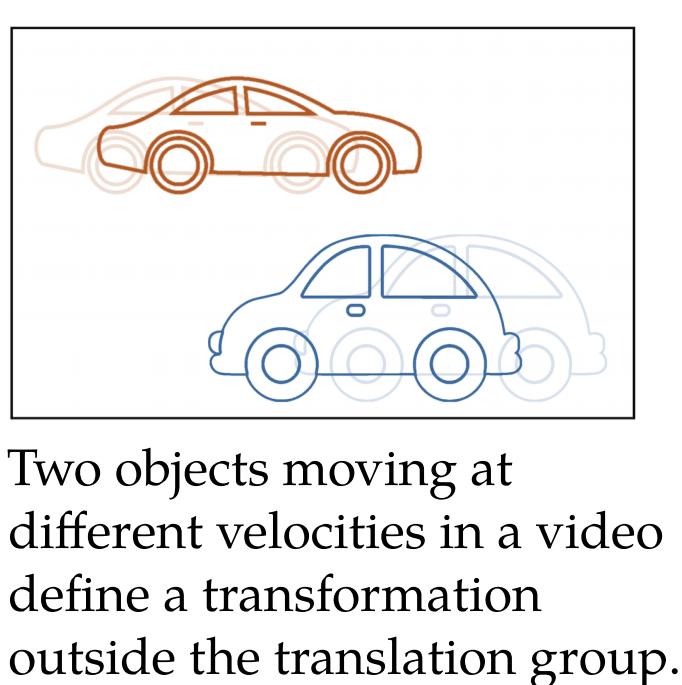
因此我们的网络应该要构建一个这样的不变群能够囊括这种不变转换,即有别于旋转平移对称的常规操作,另外,对于不变群的边界也应该有延伸和评估: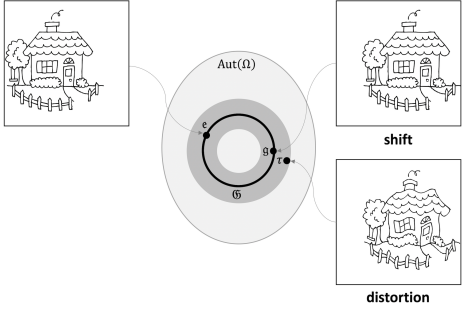
这样才能做到比卷积网络强的多的稳定性。除了这些显而易见的优越性,几何深度学习指出,目前从底层来说,神经网络都是假设把高维问题映射到低维问题上的,虽然映射后信息会有所损失,但是足以解决大多数问题:

但是 ,损失的信息伴随的不仅仅是有一些精确度上的问题,对于大规模大维数的问题,这种映射就更显得无力,因为随着维数的扩大,拟合真实函数F()的问题显得非常困难(红点是样本,蓝线是拟合函数):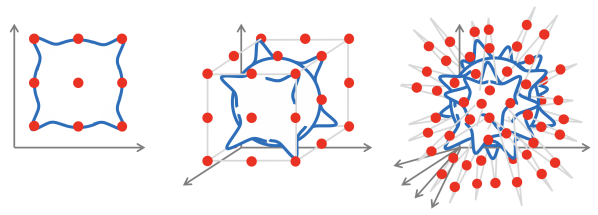
对于这种拟合函数复杂度爆炸的问题,几何深度学习就得心应手,因为刚才说过,通过群变换这种结构化数据可以衍生出许多样本,缺少抽样的问题不再那么困难。
更正式地,几何深度学习研究的是一个(物理)空间域Ω,一个信号空间X (Ω), 和一个假定的函数家族 F(X (Ω)) 。最核心的操作有两个,