总结: 我总是从迷你程序中学到很多。这个教程用python写了一个很简单迷你程序讲解递归神经网络。
递归神经网络即RNN和一般神经网络有什么不同?出门左转我们一篇博客已经讲过了传统的神经网络不能够基于前面的已分类场景来推断接下来的场景分类,但是RNN确有一定记忆功能。废话少说,上图:
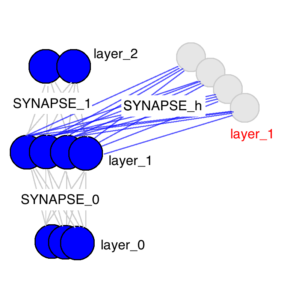
layer_0就是输入层,layer_1就是隐层,layer_2就是输出层。什么叫隐层呢?顾名思义,隐层就是隐藏层,训练时对外是透明的,毕竟主要关心的还是输出层的判断结果。这里RNN和一般神经网络不一样的是多了一个隐层,有没有发现layer_1有两个呢?是的,这一个红色的多出来的类似缓存的layer_1就是RNN的独特之处。SYNAPSE_0, SYNAPSE_1, SYNAPSE_h分别是输入层,输出层和隐层的权重值矩阵,模型训练的也主要是这些矩阵的权重值。
所以,RNN的关键就是:
每次的隐层值不再只是layer_0![]() SYNAPSE_0 ,而是 layer_0
SYNAPSE_0 ,而是 layer_0![]() SYNAPSE_0和layer_1
SYNAPSE_0和layer_1![]() SYNAPSE_h 的叠加。即,每次隐层的计算是上一次隐层值和附加隐层权重SYNAPSE_h点乘叠加上这次隐层值。
SYNAPSE_h 的叠加。即,每次隐层的计算是上一次隐层值和附加隐层权重SYNAPSE_h点乘叠加上这次隐层值。
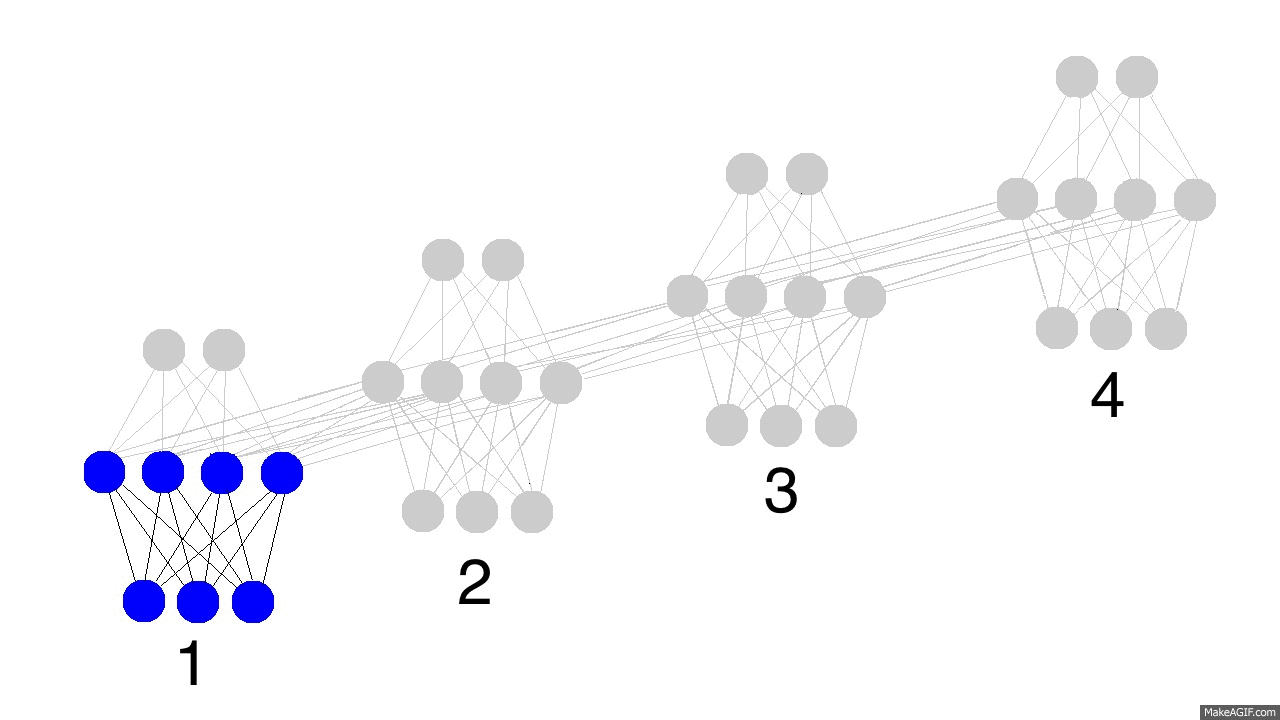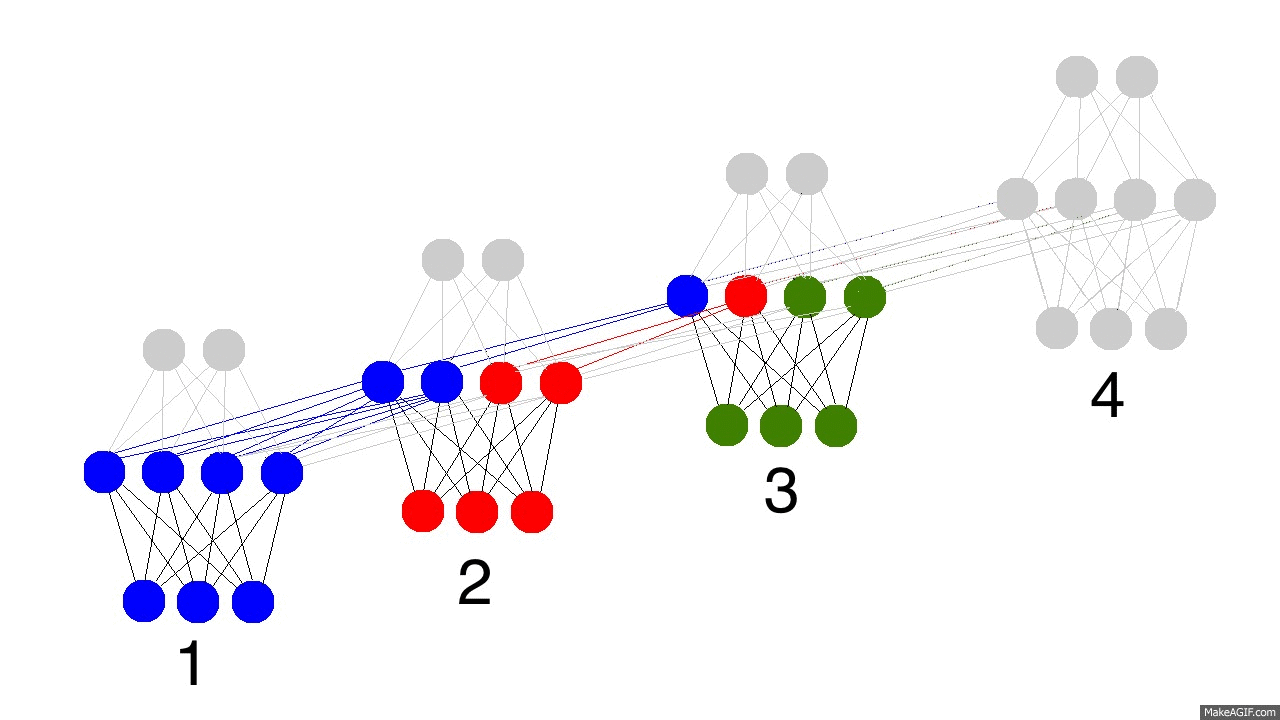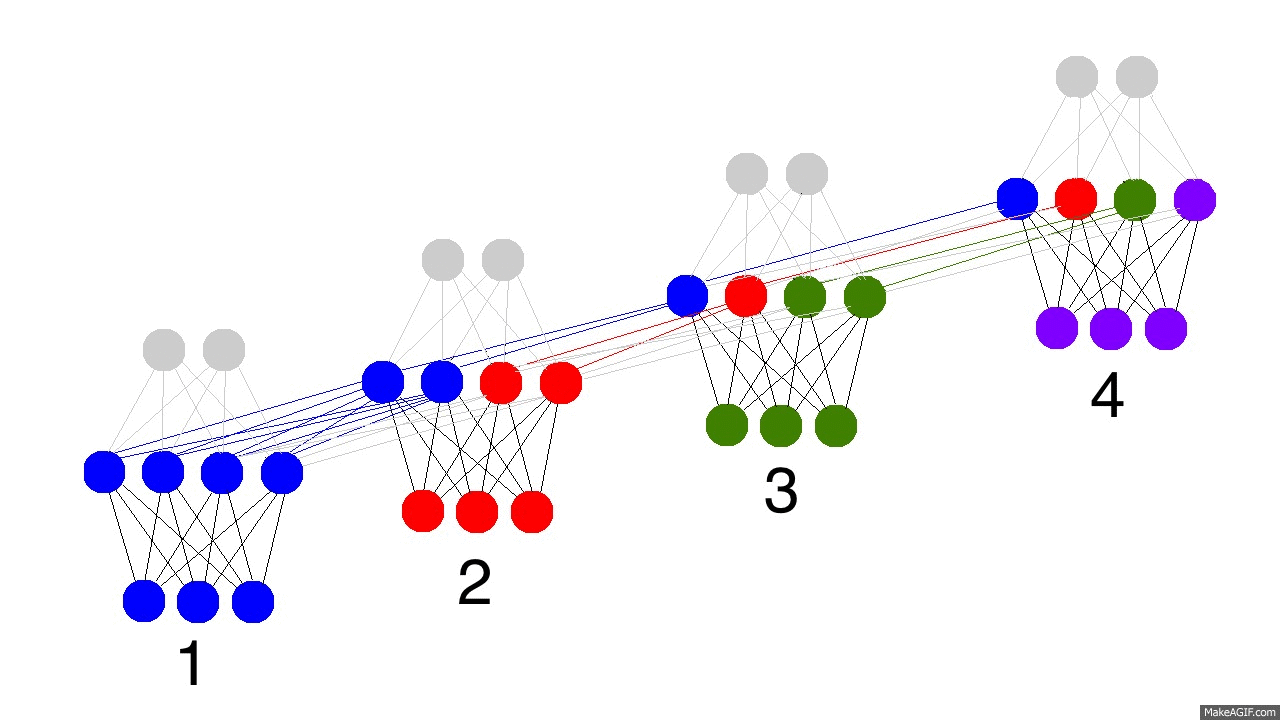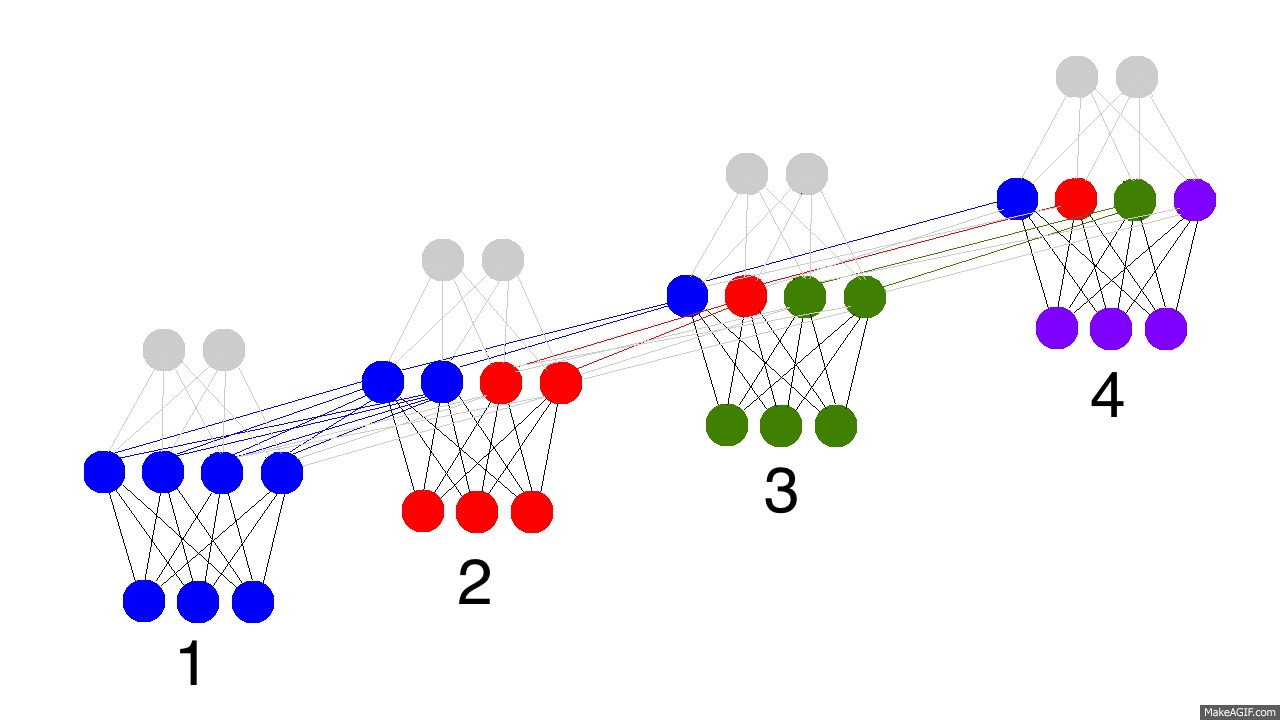
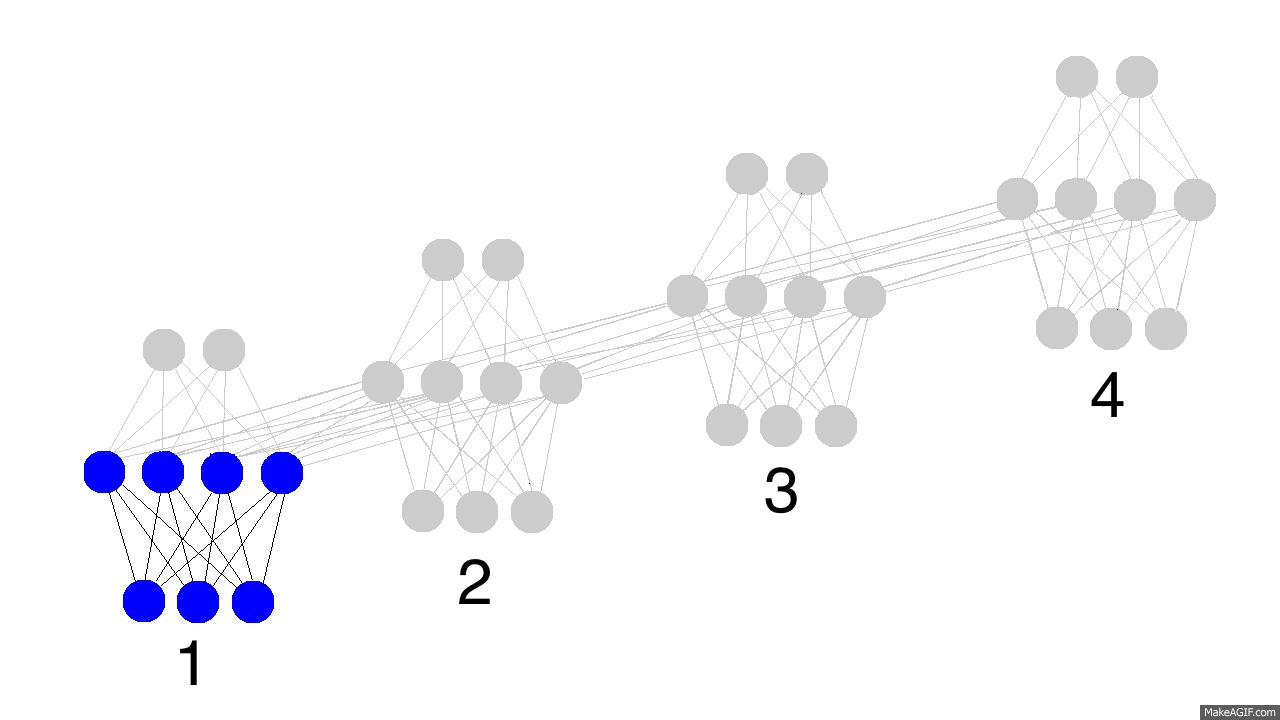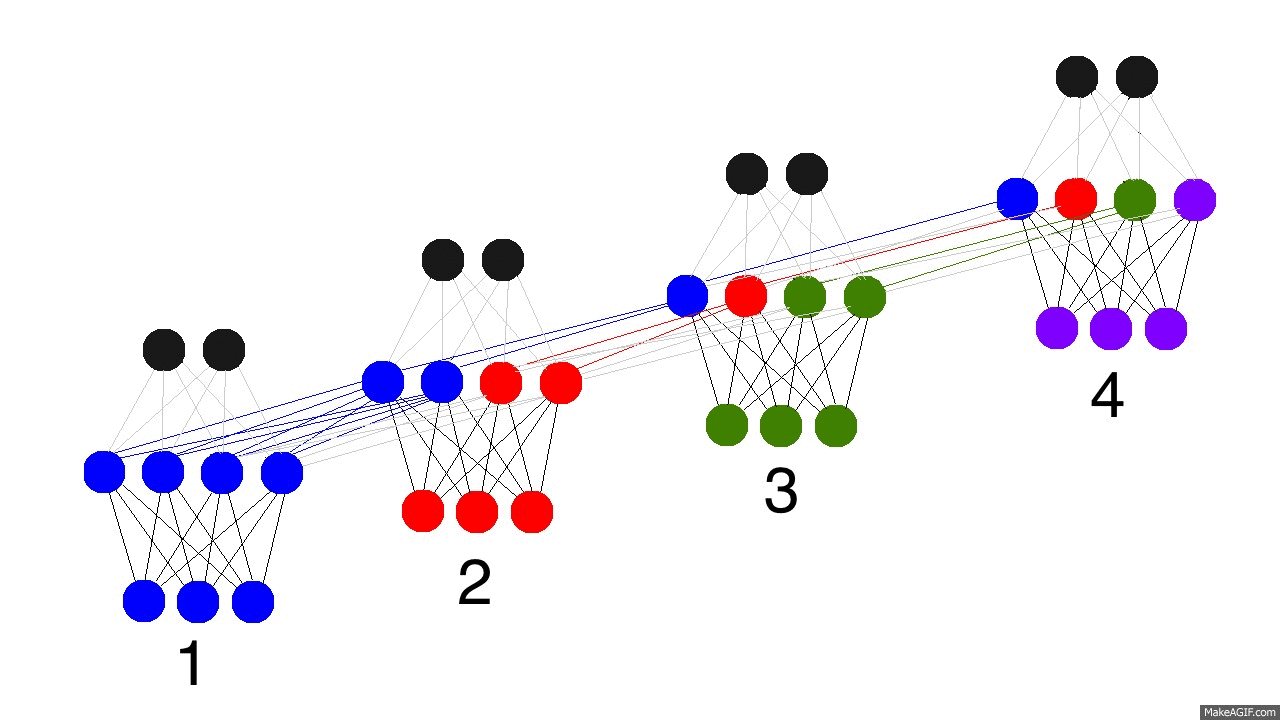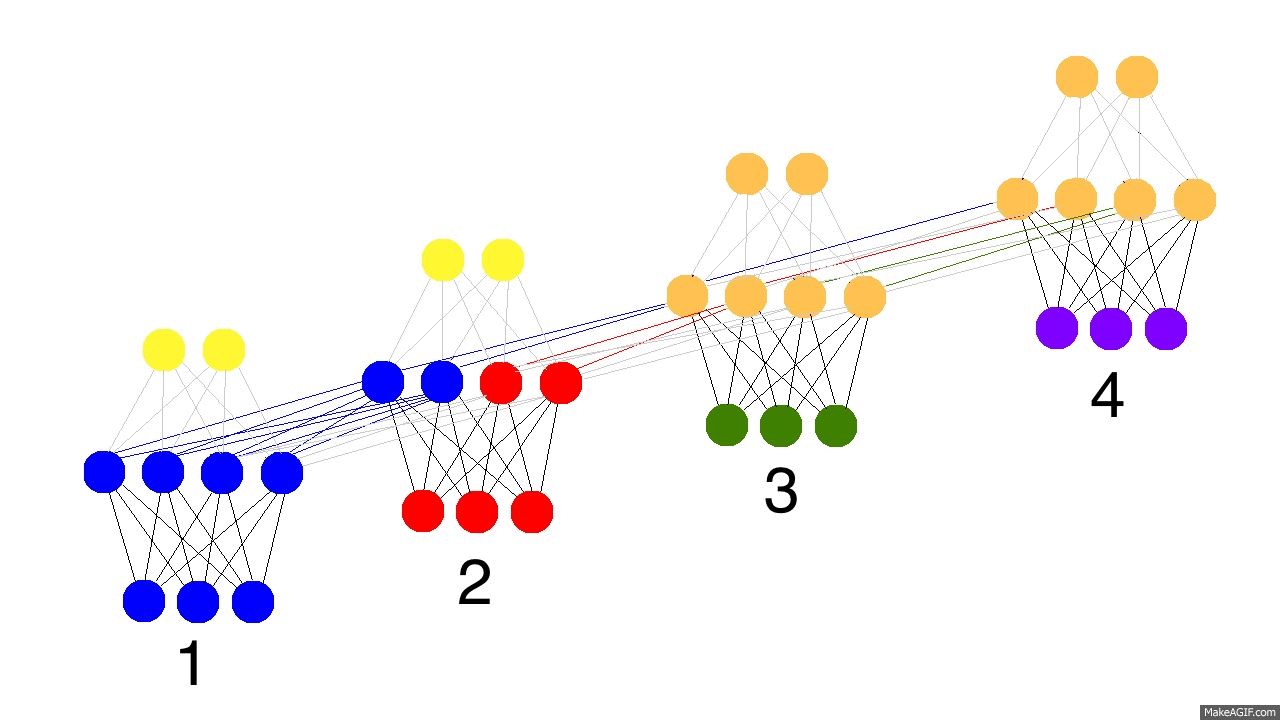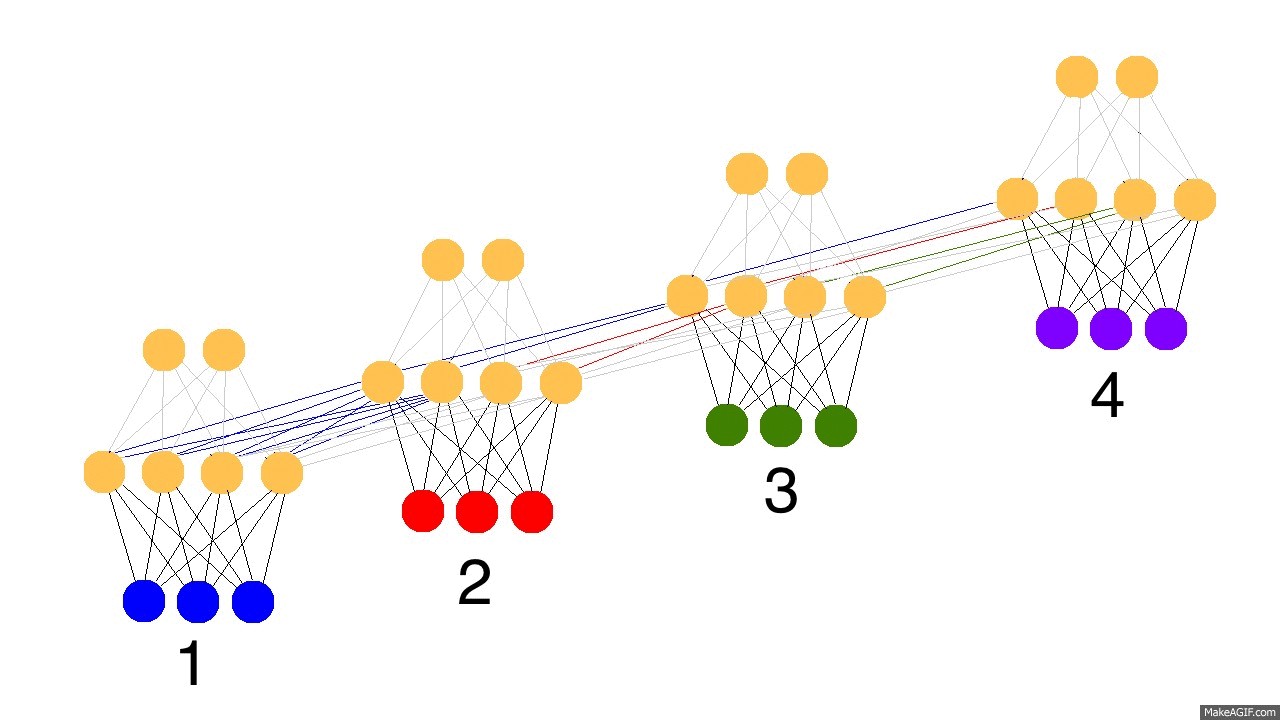
上图展示了训练隐层的四个时间戳过程,值得注意的是,每次隐层都会保留之前输入信息,并且和此次输入层信息叠加成新的信息,再和下一次输入叠加。这就导致最后隐层包含了各种颜色的信息。而且,隐层会“遗忘”那些不重要的信息,如时间戳3把红色和紫色信息较多地“遗忘”。
上图是反向传播的修正过程,黑色是预测值,亮黄色是错误,橘黄色是求导值,通过求导值对各个时间戳上的权衡矩阵做修正。
具体怎么实现呢?废话少说, 上代码:
import copy, numpy as np
np.random.seed(0)
# compute sigmoid nonlinearity
def sigmoid(x):
output = 1/(1+np.exp(-x))
return output
# convert output of sigmoid function to its derivative
def sigmoid_output_to_derivative(output):
return output*(1-output)
# training dataset generation
int2binary = {}
binary_dim = 8
largest_number = pow(2,binary_dim)
binary = np.unpackbits(
np.array([range(largest_number)],dtype=np.uint8).T,axis=1)
for i in range(largest_number):
int2binary[i] = binary[i]
# input variables
alpha = 0.1
input_dim = 2
hidden_dim = 16
output_dim = 1
# initialize neural network weights
synapse_0 = 2*np.random.random((input_dim,hidden_dim)) - 1
synapse_1 = 2*np.random.random((hidden_dim,output_dim)) - 1
synapse_h = 2*np.random.random((hidden_dim,hidden_dim)) - 1
synapse_0_update = np.zeros_like(synapse_0)
synapse_1_update = np.zeros_like(synapse_1)
synapse_h_update = np.zeros_like(synapse_h)
# training logic
for j in range(10000):
# generate a simple addition problem (a + b = c)
a_int = np.random.randint(largest_number/2) # int version
a = int2binary[a_int] # binary encoding
b_int = np.random.randint(largest_number/2) # int version
b = int2binary[b_int] # binary encoding
# true answer
c_int = a_int + b_int
c = int2binary[c_int]
# where we'll store our best guess (binary encoded)
d = np.zeros_like(c)
overallError = 0
layer_2_deltas = list()
layer_1_values = list()
layer_1_values.append(np.zeros(hidden_dim))
# moving along the positions in the binary encoding
for position in range(binary_dim):
# generate input and output
X = np.array([[a[binary_dim - position - 1],b[binary_dim - position - 1]]])
y = np.array([c[binary_dim - position - 1]]).T
# hidden layer (input ~+ prev_hidden)
layer_1 = sigmoid(np.dot(X,synapse_0) + np.dot(layer_1_values[-1],synapse_h))
# output layer (new binary representation)
layer_2 = sigmoid(np.dot(layer_1,synapse_1))
# did we miss?... if so, by how much?
layer_2_error = y - layer_2
layer_2_deltas.append((layer_2_error)*sigmoid_output_to_derivative(layer_2))
overallError += np.abs(layer_2_error[0])
# decode estimate so we can print it out
d[binary_dim - position - 1] = np.round(layer_2[0][0])
# store hidden layer so we can use it in the next timestep
layer_1_values.append(copy.deepcopy(layer_1))
future_layer_1_delta = np.zeros(hidden_dim)
for position in range(binary_dim):
X = np.array([[a[position],b[position]]])
layer_1 = layer_1_values[-position-1]
prev_layer_1 = layer_1_values[-position-2]
# error at output layer
layer_2_delta = layer_2_deltas[-position-1]
# error at hidden layer
layer_1_delta = (future_layer_1_delta.dot(synapse_h.T) + layer_2_delta.dot(synapse_1.T)) * sigmoid_output_to_derivative(layer_1)
# let's update all our weights so we can try again
synapse_1_update += np.atleast_2d(layer_1).T.dot(layer_2_delta)
synapse_h_update += np.atleast_2d(prev_layer_1).T.dot(layer_1_delta)
synapse_0_update += X.T.dot(layer_1_delta)
future_layer_1_delta = layer_1_delta
synapse_0 += synapse_0_update * alpha
synapse_1 += synapse_1_update * alpha
synapse_h += synapse_h_update * alpha
synapse_0_update *= 0
synapse_1_update *= 0
synapse_h_update *= 0
# print out progress
if(j % 1000 == 0):
print "Error:" + str(overallError)
print "Pred:" + str(d)
print "True:" + str(c)
out = 0
for index,x in enumerate(reversed(d)):
out += x*pow(2,index)
print str(a_int) + " + " + str(b_int) + " = " + str(out)
print "------------"
代码输出:
Error:[ 3.45638663] Pred:[0 0 0 0 0 0 0 1] True:[0 1 0 0 0 1 0 1] 9 + 60 = 1 ------------ Error:[ 3.63389116] Pred:[1 1 1 1 1 1 1 1] True:[0 0 1 1 1 1 1 1] 28 + 35 = 255 ------------ Error:[ 3.91366595] Pred:[0 1 0 0 1 0 0 0] True:[1 0 1 0 0 0 0 0] 116 + 44 = 72 ------------ Error:[ 3.72191702] Pred:[1 1 0 1 1 1 1 1] True:[0 1 0 0 1 1 0 1] 4 + 73 = 223 ------------ Error:[ 3.5852713] Pred:[0 0 0 0 1 0 0 0] True:[0 1 0 1 0 0 1 0] 71 + 11 = 8 ------------ Error:[ 2.53352328] Pred:[1 0 1 0 0 0 1 0] True:[1 1 0 0 0 0 1 0] 81 + 113 = 162 ------------ Error:[ 0.57691441] Pred:[0 1 0 1 0 0 0 1] True:[0 1 0 1 0 0 0 1] 81 + 0 = 81 ------------ Error:[ 1.42589952] Pred:[1 0 0 0 0 0 0 1] True:[1 0 0 0 0 0 0 1] 4 + 125 = 129 ------------ Error:[ 0.47477457] Pred:[0 0 1 1 1 0 0 0] True:[0 0 1 1 1 0 0 0] 39 + 17 = 56 ------------ Error:[ 0.21595037] Pred:[0 0 0 0 1 1 1 0] True:[0 0 0 0 1 1 1 0] 11 + 3 = 14 ------------
手把手解释代码:
0-2行: 导入所需库,初始化随机生成器。Numpy是做代数的强大库。
4-11行: 我们的激活函数和求导函数。详细请看文章Neural Network Tutorial
15行: 我们做个映射,把一个整数映射到一串比特串。比特串的每一位作为RNN的输入。
16行: 比特串的最大长度。
18行: 计算8位比特串最大可能表示的整数。
19行: int2binary和binary都是一个从整数到比特串的表示查找表。这样比较清晰。
26行: 学习步长设置为0.1。
27行: 每次我们喂给RNN的输入数据是两个比特。
28行: 这是隐层的比特数。也可以说是隐层神经元个数。隐层神经元个数如何影响收敛速度? 读者可以自行研究~
29行: 输出层我们仅仅预测一位求和值。
33行: 这是输入层和隐层间的权重矩阵。所以就是输入层单元*隐层单元的矩阵(2 x 16 )。
34行: 这是隐层和输出层间的权重矩阵。所以就是隐层单元*输出层单元的矩阵(16*1 )。
35行: 这是连接上一个时间戳隐层和当前时间戳隐层的矩阵,同时也是连接当前时间戳隐层和下一个时间戳隐层的矩阵。所以矩阵是隐层单元*隐层单元(16 x 16)。
37 – 39行: 这些变量保存对于权重矩阵的更新值,我们的目的不就是训练好的权重矩阵吗?我们在每次迭代积累权重更新值,然后一起更新。
42行: 我们要迭代训练100,000个训练样本。
45行: 我们将要生成一个随机加和问题。我随机生成的整数不会超过我们所能表达的整数的一半,否则两个整数相加就有可能超过我们可以用比特串表达的整数。
46行: 查找整数a对应的比特串。
48行: 和45行类似
49行: 和46行类似
52行: 计算应该得出结果。
53行: 查找计算结果对应的比特串
56行: 得到一个空的比特串来存储我们RNN神经网络的预测值。
58行: 初始化错误估计,作为收敛的依据。
60-61行: 这两个列表是在每个时间戳跟踪输出层求导和隐层值的列表。
62行: 开始时没有上一个时间戳隐层,所有我们置为0.
65行: 这个迭代可能的比特串表达(8位比特串)。
68行: X就像是文章开头图片中的”layer_0″. X 是一个2个元素的列表,第一个元素是比特串a中的,第二个元素是比特串b中的。我们用position定位比特位,是自右向左的。
69行: 和62类似,我们的正确结果 (1或0)
72行: 这行是代码申神奇之处!!! 请看懂这一行!!! 为了构造隐层,我们做两件事,第一步是从输入层传播到隐层(np.dot(X,synapse_0))。第二步,我们把上一个时间戳的隐层值传播到当前隐层 (np.dot(prev_layer_1, synapse_h)。最后我们把两个向量值相加! 最后交给sigmoid函数.
75行: 这行很简单,把隐层传播到输出层,做预测。
78行: 计算预测的错误偏差。
79行: 计算并存储错误导数,在每个时间戳进行.
80行: 计算错误的绝对值的和,积累起来。
83行: 估计输出值。并且保存在d中。
86行: 保存当前隐层值,作为下个时间戳的上个隐层值。
90行: 所以,我们对于所有的时间戳做了前向传播,我们计算了输出层的求导并且把它们存在列表中。现在我们需要反向传播,从最后一个时间戳开始反向传播到第一个时间戳。
92行: 像我们之前一样获得输入数据。
93行: 选择当前隐层。
94行: 选择上个时间戳隐层。
97行: 选择当前输出错误。
99行: 这行在给定下一个时间戳隐层错误和当前输出错误的情况下,计算当前隐层错误。
102-104行: 现在我们在当前时间戳通过反向传播得到了求导,我们可以构造权重更新了(但暂时不更新权重)。我们等到完全反向传播后,才真正去更新权重。为什么?因为反向传播也是需要权重的。乱改权重是不合理的。
109 – 115行 现在我们反向传播完毕,可以真的更新所有权重了。
118行 – 最后 一些log和输出看结果。
翻译编辑自:https://iamtrask.github.io/2015/11/15/anyone-can-code-lstm/
David 9
Latest posts by David 9 (see all)
- 修订特征已经变得切实可行, “特征矫正工程”是否会成为潮流? - 27 3 月, 2024
- 量子计算系列#2 : 量子机器学习与量子深度学习补充资料,QML,QeML,QaML - 29 2 月, 2024
- “现象意识”#2:用白盒的视角研究意识和大脑,会是什么景象?微意识,主体感,超心智,意识中层理论 - 16 2 月, 2024
《#7 每个人都能徒手写递归神经网络–手把手教你写一个RNN》上有1条评论