如果AI的本质是在可接受时间内搜索到最优解,那么容易定义最优解的问题都是AI可以解决的。这样,人类的“情感”看起来如此“珍贵”,因为它很难用人工定义“最优解” — David 9
相信大家还记得2017年初人工智能Libratus完胜德州扑克顶级玩家的事,年底卡耐基梅隆大学(CMU)在NIPS 2017上公开这一贡献并获得最佳论文奖。这一进展之所以让人兴奋,是因为它为不完美信息博弈(Imperfect-Information Games)问题提供了新的解决思路:

像棋类游戏,双方都是共享一切信息的,这种博弈称为完美信息博弈。而扑克类,谈判,商业决策等类似问题,双方的信息都是不公开给对方的,这就提高了AI算法搜索最优解的难度。
对于完美信息博弈,每一步Action引出下一步子状态,接下来在子状态中求解最优解即可:

对于不完美信息博弈,我们不能安心地解决眼前的子问题,因为我们同时必须考虑:“对手的手牌现在会是什么样的?”,“他下一次会用什么策略?”等等烦人的问题,因此许多平行的子问题是我们必须同时考虑的:
CMU的学者通过求解安全嵌套子博弈的方法改进了之前的扑克算法。
值得强调的是,该论文算法的许多思想都是继承了前人求解子博弈的方法论,包括对纳什均衡重点关注。
纳什均衡是让博弈双方在自己的角度都没有更好策略的状态,如果对方稍微调整策略,他就会得到更坏的结果,对我方来说亦然。在算法中关注纳什均衡可以提高算法的鲁棒性,使得玩家不容易找到博弈中的破绽,OpenAI的Dota算法和AlphaGo都说明了鲁棒性在游戏中的重要性(人类总是试图在游戏中找到机器的破绽):
那么,求解安全嵌套子博弈 的算法,究竟是如何“安全”,又如何“嵌套”的呢?让我们先从“安全”开始说起。
首先,我们先建立一个简单的博弈模型。
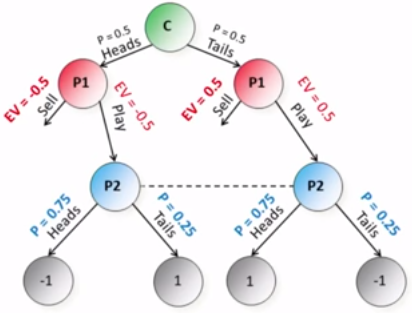
这是P1和P2两个人之间的抛硬币游戏。P1可以投一次硬币,正反只有自己可以看到,抛完之后他可以选择卖掉硬币(如果正面他选择卖掉硬币,那他就得0.5分,如果是反面他还要卖掉,那就扣0.5分),此外,他还可以和P2进行游戏,让他猜一下正反,如果他猜对P1扣1分,如果猜错,P1加1分:
显然,这时对于P2来说他在玩一个不完美信息的子博弈,他看不到P1抛硬币的结果,但是P1卖掉硬币的回报(正面0.5,反面-0.5)却和整个游戏息息相关:
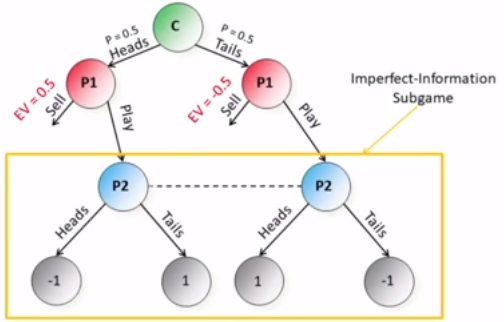
这时如果P2总是猜正面,P1在抛到正面时肯定会卖掉硬币得到0.5分,如果抛到反面,P1肯定会选择和P2玩游戏,并且P2猜错,就能得到1分。所有P1的期望分数是0.5*0.5+0.5*1=0.75
而,如果P2总是猜反面,P1在抛到正面时肯定会和P2玩游戏,P2猜错 ,P1得1分;如果P1抛到反面,那他还不如卖掉硬币只扣0.5分(而不是1分),所以P1的期望分数是:
0.5*1+0.5*(-0.5)= 0.25
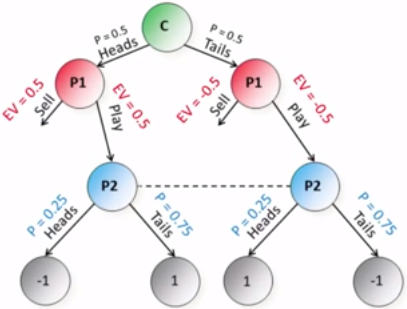
事实上,P2可以很牛B地采取以下策略达到纳什均衡:
P2以0.25的概率猜正面,以0.75的概率猜反面。
这样P1如果抛到正面,无论卖掉硬币还是和P2玩游戏,都是0.5分的回报;如果抛到反面,无论如何,也都是-0.5的回报,所以,总回报是0:
这时,对于P2来说,如果不考虑P1卖掉硬币的回报,就是一个不安全博弈。
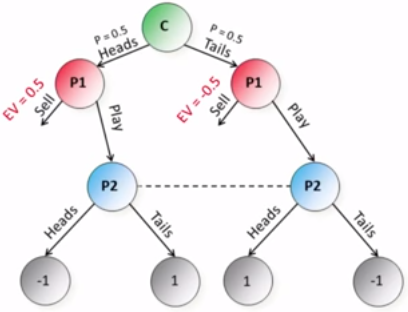
试想,如果游戏规则变了,P1卖掉正面硬币的回报是 -0.5,而卖掉反面硬币的回报是0.5,而对于P2他看不到P1行为的任何变化(虽然P1所处的环境发生了改变)如下:
这时,P2的最优解就应该变成:
P2以0.75的概率猜正面,以0.25的概率猜反面。
甚至,在日常买菜的谈判中也是如此,哪怕今天的菜价不变,你也会寻求其他隐形的理由在买菜时砍价。
如果一味地猜测P1的策略也是不现实的,因为当P2的策略改变,P1的策略也能随之改变。
对P2来说,比较安全的方法是,猜测P1卖掉硬币时的回报,并且不断更新这一猜测值,在猜测值的子问题下,寻求更优解,如此嵌套下去:

以上是David 9对本论文的一些见解,如果大家有更深入的见解欢迎联系David 9进一步探讨。
参考文献:
- http://papers.nips.cc/paper/6671-safe-and-nested-subgame-solving-for-imperfect-information-games.pdf
- https://www.youtube.com/watch?v=tRiaGahlyy4
- https://www.youtube.com/watch?v=EbKmZLp5HvA
本文采用署名 – 非商业性使用 – 禁止演绎 3.0 中国大陆许可协议进行许可。著作权属于“David 9的博客”原创,如需转载,请联系微信: david9ml,或邮箱:yanchao727@gmail.com
或直接扫二维码:
David 9
Latest posts by David 9 (see all)
- 修订特征已经变得切实可行, “特征矫正工程”是否会成为潮流? - 27 3 月, 2024
- 量子计算系列#2 : 量子机器学习与量子深度学习补充资料,QML,QeML,QaML - 29 2 月, 2024
- “现象意识”#2:用白盒的视角研究意识和大脑,会是什么景象?微意识,主体感,超心智,意识中层理论 - 16 2 月, 2024