入门机器学习, 总有几张图片, 令人印象深刻. 以下是十张经典图片, 图解机器学习, 非常有 启发性:
1. 训练错误和测试错误。这张图告诉我们训练错误越小,不一定是最好的。训练误差和测试误差要达到一个平衡,才是最好的。下图展示了ESL 图 2.11, 训练错误和测试错误与模型复杂度的关系.
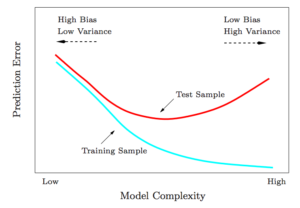
2. “欠拟合”和”过拟合”. 出自PRML 图1.4. 下图数据点是从绿色曲线生成的. 拟合参数是M, 通过M得到的模型是红色曲线. 可见, 如果M过小, 得到的模型不够复杂, 不能还原真实模型, 也就是”欠拟合”. 如果M太大, 得到的曲线复杂度过高, 也不能真实还原模型, 也就是”过拟合”. 猜到了吧? 还是要在”欠拟合”和”过拟合”之间找到一个平衡呀~
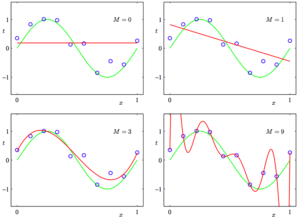
3. 奥卡姆剃刀(Occam’s razor). 出自ITILA 图 28.3. 为什么贝叶斯推断包含着奥卡姆剃刀的原理 ? 下图展示了为什么复杂的模型会变得低效。横轴代表了贝叶斯理论的汇报模型在可能数据集上被准确预测的可能性。![]() 代表了使用复杂模型
代表了使用复杂模型![]() 情况下,数据集
情况下,数据集![]() 被准确预测的概率和置信度(Evidence);
被准确预测的概率和置信度(Evidence);![]() 代表了使用较简单模型
代表了使用较简单模型![]() 情况下,数据集
情况下,数据集![]() 被准确预测的概率和置信度(Evidence)。可见复杂模型
被准确预测的概率和置信度(Evidence)。可见复杂模型![]() 在预测时,一些数据置信度,或者信心很高,但是其实整体准确度, 不如模型
在预测时,一些数据置信度,或者信心很高,但是其实整体准确度, 不如模型![]() 。说什么来着? 模型复杂度也要平衡哦~
。说什么来着? 模型复杂度也要平衡哦~
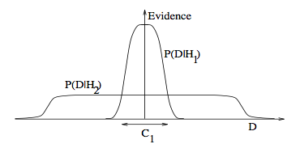
4. 特征结合。(1) 为什么投影后的特征看起来相关, 而离散个体看起来无关 ? (2) 为什么线性模型会失效? 来自Isabelle Guyon的特征抽取教程.
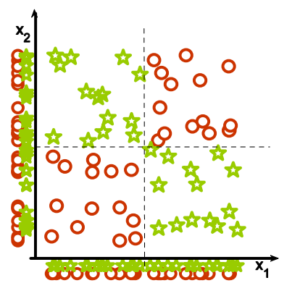
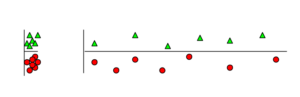
5. 无关特征. 下图中, 使用y轴作为特征区分样本, 但是, 看起来是不是右图更容易混淆? 混淆就是因为多了x轴的干扰.
6. 升维. 一个非线性的问题, 在升维之后, 可以变为一个线性问题. 如下图, 想象样本是从一维的曲线生成的, 一定是个非线性问题. 但是如果把这个曲线看做是二维的, 马上就可以用线性的基础函数划分开了. 这就是SVM(支持向量机)的理论. 来自Andrew Moore的SVM 教程 .
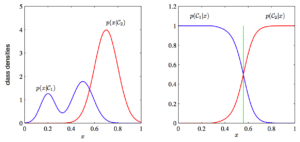
7. 判别模型和生成模型. 来自PRML 图 1.27. 左图是只使用先验的判别模型, 而右图是使用了后验的生成模型, 绿色垂直线代表最有信心的分界线.
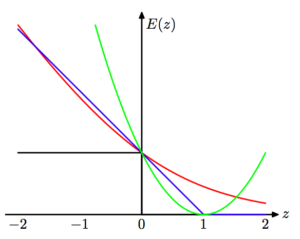
8. 损失函数. 非常多的机器学习算法可以看做优化损失函数的过程. 来自 PRML 图 7.5. 蓝线: SVM中的hinge error function. 绿线: 均方错误. 黑线:错分率. 红色: log函数回归错误.
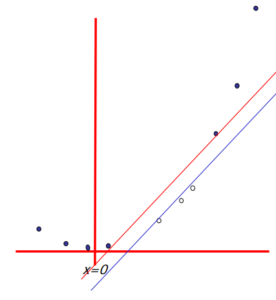
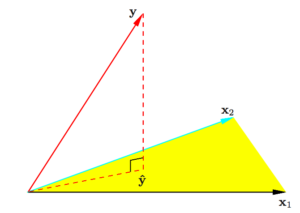
9. 最小方差的几何图解. 来自 ESL 图 3.2. y轴在平面上的投影表示最小方差估计.
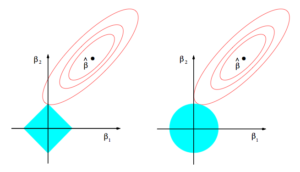
10. 稀疏性. 为什么 Lasso (L1 范数正则) 容易给出稀疏解 ? (即 权重向量有更多的零值). 来自ESL 图 3.11. 图中红色的等高线是平方误差项等值线, 可以理解为在等高线上的解是误差相等的. 左图蓝色方形线是L1范数等值线, 右图蓝色圆形线是L2范数等值线. 可见L1范数更可能得到轴上权重值为0的解. 即, 得到的解更容易稀疏.
翻译转自: Machine learning in 10 pictures
David 9
Latest posts by David 9 (see all)
- 修订特征已经变得切实可行, “特征矫正工程”是否会成为潮流? - 27 3 月, 2024
- 量子计算系列#2 : 量子机器学习与量子深度学习补充资料,QML,QeML,QaML - 29 2 月, 2024
- “现象意识”#2:用白盒的视角研究意识和大脑,会是什么景象?微意识,主体感,超心智,意识中层理论 - 16 2 月, 2024