Stanford教授Daphne Koller 概率图模型 — 终极入门 第三讲 马尔可夫网络 (Markov Networks)

贝叶斯网络中的一些基本直觉，不能直接使用到马尔可夫网络 — David 9

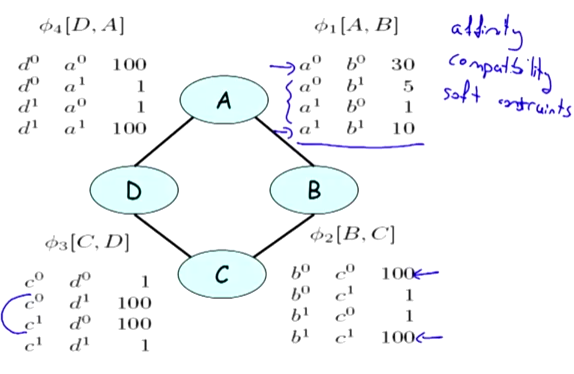
上一讲, 我们介绍了模板模型,  今天我们要把注意力放到无向图模型，以及马尔可夫网络 (Markov Networks). 事实上之所以叫做无向图模型，只是因为概率图中的边可以是双向的：

这里的Φ1[A, B] 称为一个factor(因素)。但是Φ1[A, B]并不是有用的分布。如上图， Φ1[A, B]只是代表AB边之间各种组合的概率，并不是A和B联合概率。因为A和B联合概率的取值同时也被C和D影响（仅仅一条边的情况不能说明问题）。

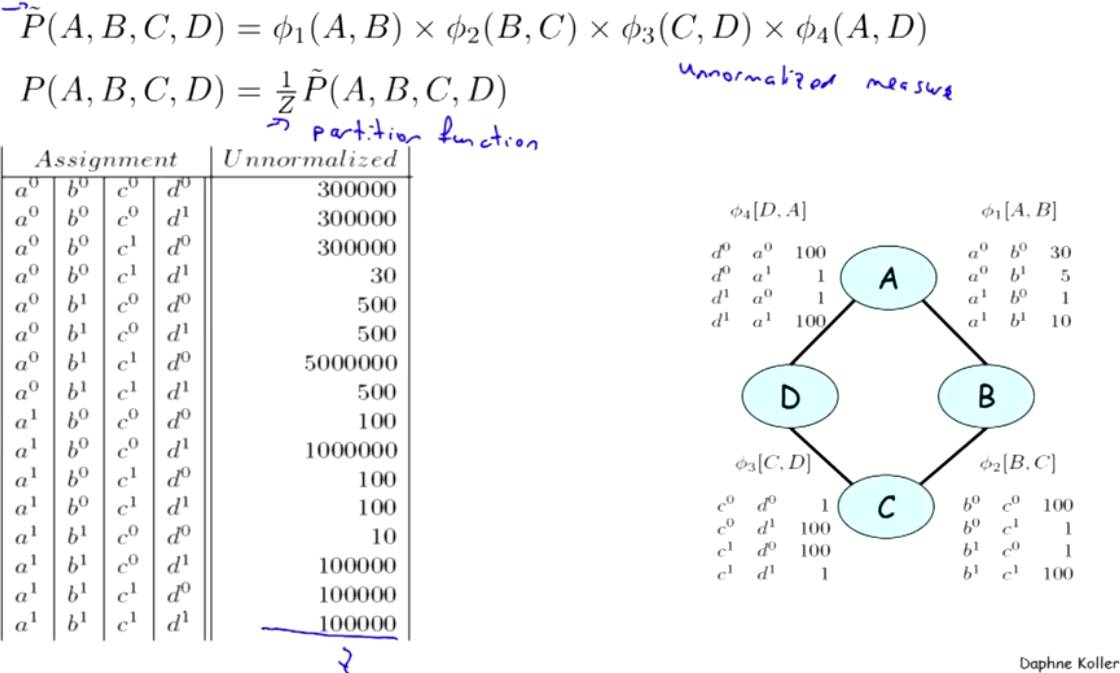
另外，不要以为 P = Φ1(A, B) * Φ2(B, C) * Φ3(C, D) * Φ4(A, D) 就是这个图的联合概率。要得到真正的联合概率P(A, B, C, D),  上面的P = Φ1(A, B) * Φ2(B, C) * Φ3(C, D) * Φ4(A, D) 还要除以一个通用的partition function：Z . 做到了规范化。

在这里，就是所有可能性值的求和：

在马尔可夫网络中，我们定义图中的每一个Φ即factor（因子），都是二元的，也就是所有因子都是成对连接的节点。我们知道，就算是全连接的图，因为马尔可夫网络是两两连接的，最大参数复杂度只能是：O(n^2*d^2) :

这里每条边只连接两个变量，所以每个factor自由度有d^2个参数（只有两个变量）.

如果factor可以有n个变量， 自由度就有d^n个参数，模型能够表达的复杂度远远大于马尔可夫网络。这就是吉布斯分布（Gibbs Distribution）：

唯一与马尔可夫网络不同的是，这里每个factor中的Di可以是多元的。

所有可以总结，

1. 马尔可夫网络和吉布斯分布都是用许多factors乘积的形式表示分布。
2. 马尔可夫网络的每个factor Φ 中只有两个变量， 而吉布斯分布有多个变量。
3. 吉布斯分布的表达能力比马尔可夫网络强。

最后我还要介绍一种非常常用的马尔可夫网络变形：条件随机场（CRF）。

与马尔可夫网络唯一不同的是，条件随机场（CRF）求partition function的时候是仅仅对一个变量求和的，最后求的是在X情况下的条件概率，而不是联合概率：

这就在建模时有许多有意思的结果：

1. CRF是很不错的判别模型， 对数几率回归就是其中一种。
2. CRF可以把整个图模型的局部特征函数转化为全局特征函数，从而写成条件随机场的权重向量和特征向量的内积形式。这就可以每次只关心一个特征。再把所有全局特征集中起来一起考虑。

如判别上图中的动物是奶牛，我们首先把整个图“切”成一块块的“小图”。

如果用贝叶斯网络或者朴素贝叶斯构建这些“小图”，就需要把每个“小图”的所有特征都考虑进去，这在最终求联合概率时将会非常复杂。而条件随机场解决了这个问题，我们不需要费力考虑每个小块之间的关系。

相反，我们可以先关注所有小块的颜色亮暗比的分布，再关注所有小块纹理粗糙度的分布，然后考虑动物边界是不是明显有4只脚，最后把这些因素都合起来，判别这个动物是不是奶牛？这样，是不是在数学上更好处理了？

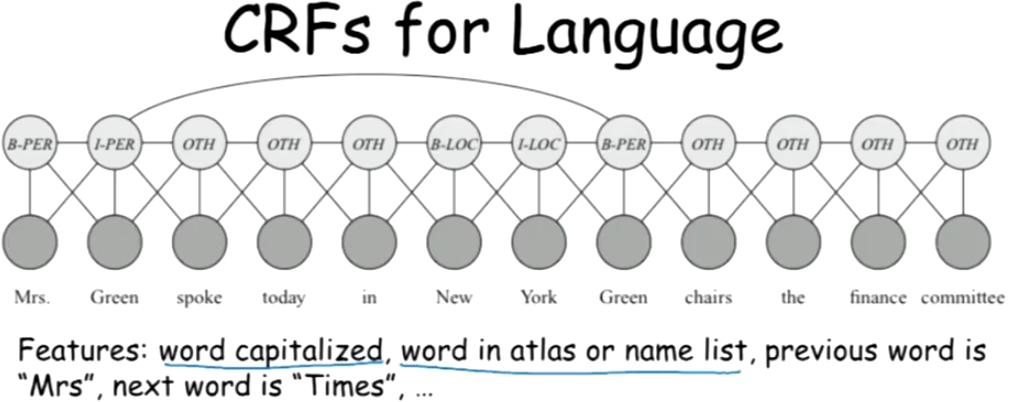
同样的，在自然语言处理中使用CRF：

我们判别一篇文章是不是科技类文章，不需要详细理解每个相邻word直接的关系。

我们可以先找出所有动词的在这篇文章的分布 ， 然后，找出所有专业名词在文章中的分布， 接着找出所有陈述句在文章中的分布（我们知道科技文章程序句非常多）。最后把这些分布结合在一起看，是不是很容易判读这篇文章是不是科技文章？

这里就是我们这一讲马尔可夫网络 (Markov Networks)的所有内容了， 敬请关注下一期内容，记得加微信（微信号：david9ml）哦~

参考文献:

1. https://www.coursera.org/learn/probabilistic-graphical-models
2. 维基百科： 马尔可夫网络
3. https://en.wikipedia.org/wiki/Graphical_model
4. http://baike.baidu.com/item/%E6%A6%82%E7%8E%87%E5%9B%BE%E6%A8%A1%E5%9E%8B
5. http://blog.csdn.net/zdy0_2004/article/details/44248083

本文章属于“David 9的博客”原创，如需转载，请联系微信david9ml，或邮箱：yanchao727@gmail.com