Stanford教授Daphne Koller 概率图模型 — 终极入门 第二讲 模板模型 (Template Models)

模板模型 , 是机器学习模型进行时空上复制的一种有效方法 — David 9

接着上一讲, 有向图模型与贝叶斯网络基础,  这一讲我们关注模板模型 (Template Models). “模板模型”在机器学习领域, 并非常用的术语, 但是在许多概率图模型中, 都有”模板模型”的影子.

所以, “模板模型”这样有价值的概率图模型抽象思想, 值得用一篇文章来解释解释.

首先, 模板模型 (Template Models)顾名思义, 是用模板的思维建立出的模型. 许多非常复杂的图模型, 事实上是可以简化的. 简化时, 通过共享通用的变量, 通用的概率图结构, 可以归纳出通用的模板模型, 达到类似复用的效果.

还记得我们讲过的动态主题模型 ? 动态主题模型正是在不同的时间点上, 复制主题模型的. 这里, 主题模型就是一个模型模型. 模版模型描述了模版变量如何从模版中继承依赖关系，同样应用的典型例子有: 动态贝叶斯模型DBN、隐马尔科夫模型HMM, 及盘模型Plate Models。

在来看一下课程试题, 加深对模板模型的印象:

模板模型的优势, 答案是选择前三点:

1. 模板模型在时序上的复制, 是有效的工具
2. 条件概率模型可以多次拷贝复制
3. 模板模型可以起到共享参数变量的作用

典型例子1, 动态贝叶斯模型DBN

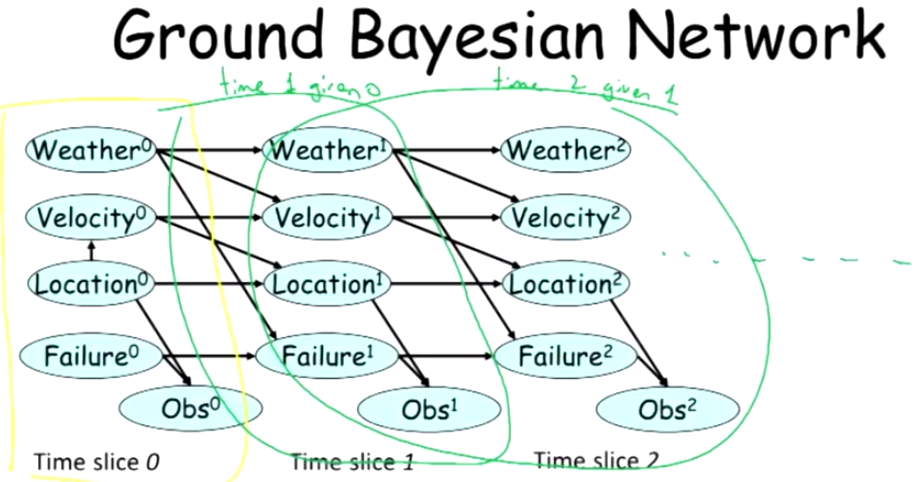
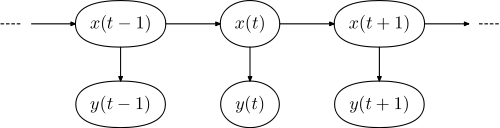
时序模型的一种就是DBN:

上图就是有3个时间片的动态贝叶斯模型DBN, 我们看到其实每个时间片的图结构是相同的复制, 但是正是因为复制模板模型, 产生了对于时间的动态建模和调参的可能.

总结DBN我们可以发现:

动态贝叶斯模型DBN, 对于长时间的时间序列轨迹的建模比较在行.

DBN有两个大大的假设:
1. 马尔科夫假设. 当前时间片模型的概率, 仅仅取决于上一个时间片的模型状态. 

2. 时间不变性假设. 时间片之间的转移概率, 不受时间影响, 仅受两个时间片的状态影响. 这就可以把模型的注意力集中在状态的转移概率上. 例如, 今天下雨, 明天也下雨的概率, 应该与100年前的某一天下雨, 次日也下雨的概率相同. 概况成公式如下:

接下来我们看看另一个使用模板模型的例子

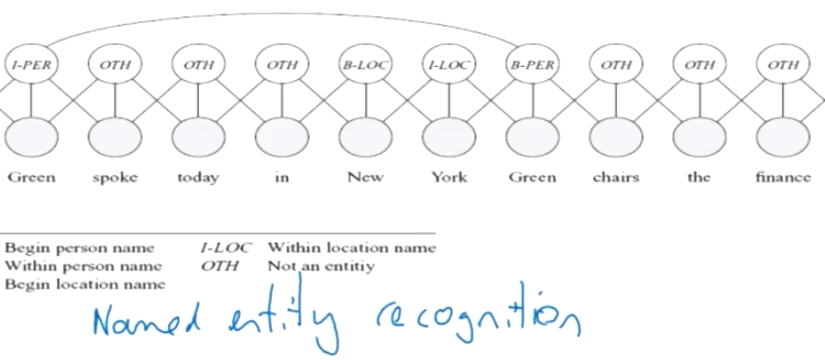
典型例子2, 隐马尔科夫模型HMM

隐马尔科夫模型就不多说了, 隐含状态, 可见状态, 转移矩阵, 等等…

值得注意的是:

1. 隐马尔科夫模型HMM其实是动态贝叶斯模型DBN的一类特殊情况(或者说子集). 因为HMM比DBN简单得多.
2. HMM不像CPD或者BN, 随机变量没有强的结构关系.
3. 因为有比较大的转移矩阵要训练, HMM显得比较稀疏, 并且重复的元素和状态非常多.

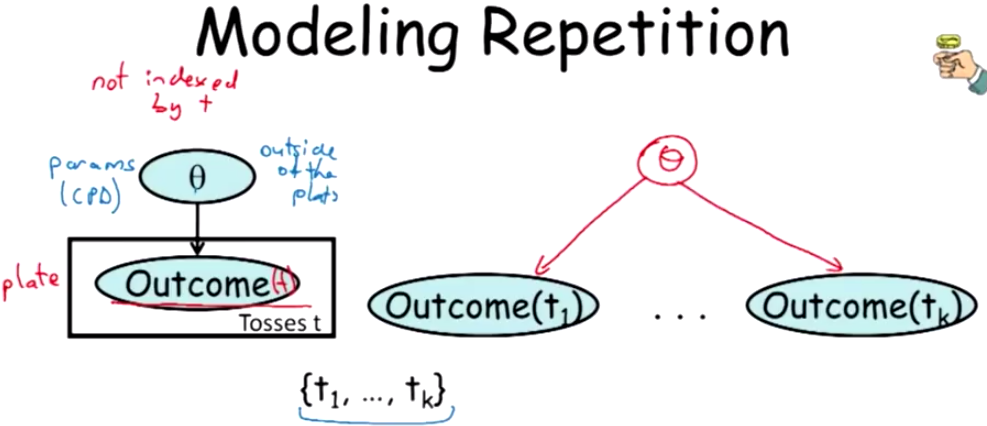
典型例子3, 盘模型(托盘模型) Plate models

如果说时序模型是通过模板模型实现时间上的复制, 那么盘模型就是通过模板模型实现空间上的复制 — David 9

学过LDA主题模型 和做过文本挖掘的同学一定熟悉这种空间上的复制. 上图左侧的盘模型, 就等同了右边的多项式分布生成的多个Outcome (从t1 到 tk). 左图的主题模型把多个Outcome简化地放在一个Tosses 盘中， 清晰地简化了表达。

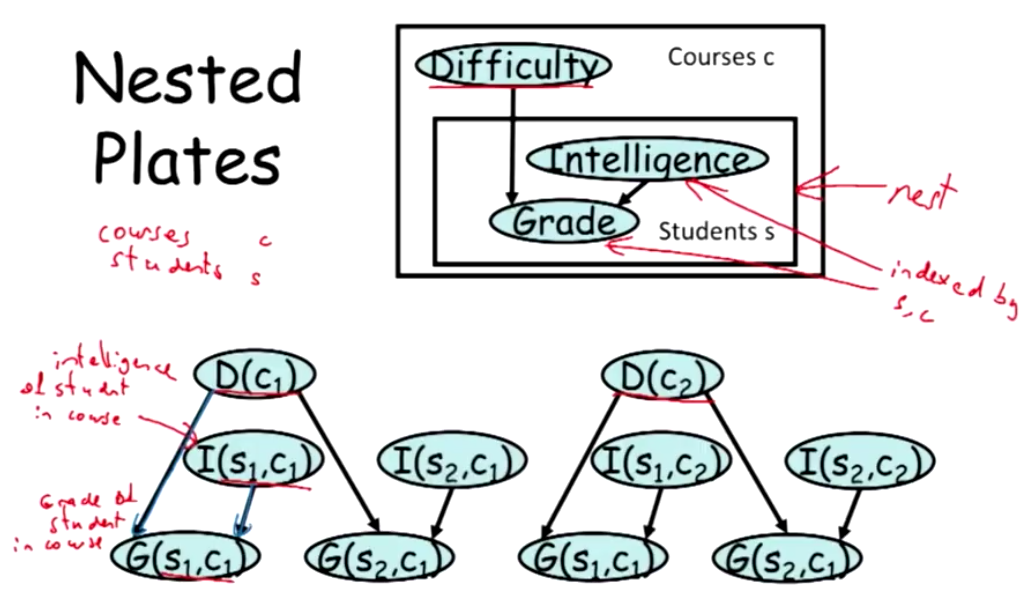
更有意思的，盘与盘之间是可以嵌套的：

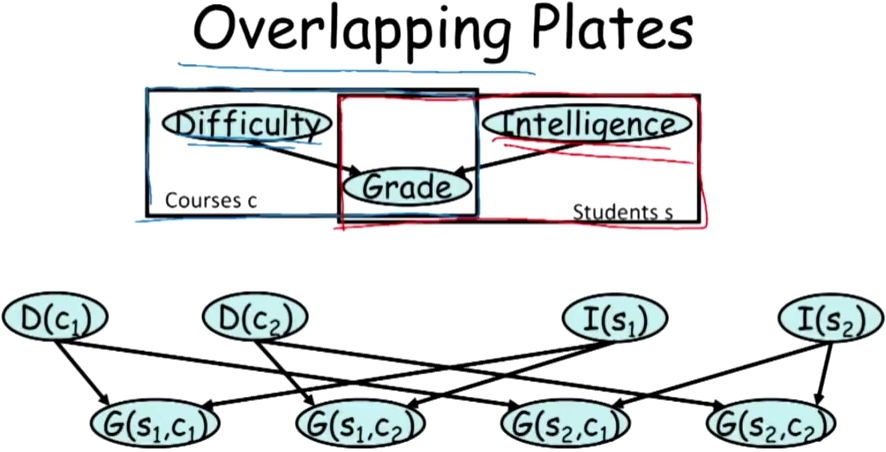
并且，盘与盘之间是可以叠加的：

这里叠加时的Grade随机变量就必须结合两个父节点的各种组合结果。

这里就是我们这一讲模板模型 (Template Models)的所有内容了， 敬请关注下一期内容，记得加david 9微信（微信号：david9ml）哦。

 

参考文献:

1. https://www.coursera.org/learn/probabilistic-graphical-models
2. http://blog.csdn.net/yangliuy/article/details/8091630
3. https://en.wikipedia.org/wiki/Graphical_model
4. http://baike.baidu.com/item/%E6%A6%82%E7%8E%87%E5%9B%BE%E6%A8%A1%E5%9E%8B
5. http://blog.csdn.net/zdy0_2004/article/details/44248083

本文章属于“David 9的博客”原创，如需转载，请联系微信david9ml，或邮箱：yanchao727@gmail.com