David 9的博客 — 不怕"过拟合"

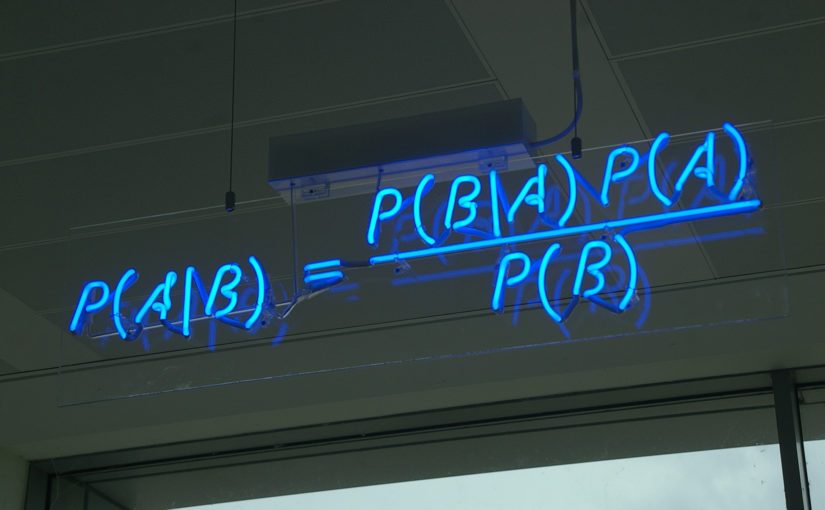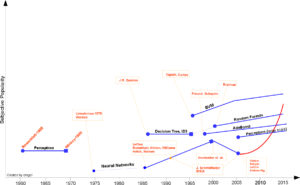
Since the initial standpoint of science, technology and AI, scientists following Blaise Pascal and Von Leibniz ponder about a machine that is intellectually capable as much as humans. Famous writers like Jules

Machine Learning is one of the important lanes of AI which is very spicy hot subject in the research or industry. Companies, universities devote many resources to advance their knowledge. Recent advances in the field propel very solid results for different tasks, comparable to human performance (98.98% at Traffic Signs – higher than human-).

Here I would like to share a crude timeline of Machine Learning and sign some of the milestones by no means complete. In addition, you should add “up to my knowledge” to beginning of any argument in the text.

First step toward prevalent ML was proposed by Hebb , in 1949, based on a neuropsychological learning formulation. It is called Hebbian Learning theory. With a simple explanation, it pursues correlations between nodes of a Recurrent Neural Network (RNN). It memorizes any commonalities on the network and serves like a memory later. Formally, the argument states that;

Let us assume that the persistence or repetition of a reverberatory activity (or “trace”) tends to induce lasting cellular changes that add to its stability.… When an  axon  of cell  A is near enough to excite a cell  B and repeatedly or persistently takes part in firing it, some growth process or metabolic change takes place in one or both cells such that  A’s efficiency, as one of the cells firing  B, is increased.[1]

In 1952 , Arthur Samuel at IBM, developed a program playing Checkers . The program was able to observe positions and learn a implicit model that gives better moves for the latter cases. Samuel played so many games with the program and observed that the program was able to play better in the course of time.
继续阅读Brief History of Machine Learning 机器学习简史