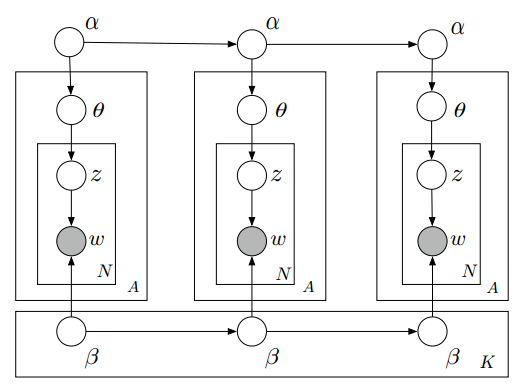
卡内基梅隆大学（CMU），那些经受住时间考验的机器学习论文–第二弹：动态主题模型

这一弹，接着上一期，这次，我们要解释一种典型的机器学习算法——动态主题模型（Dynamic Topic Model）。

概率主题模型和概率图模型是每个做文本挖掘的学者的必学课题。其中最常见的主题模型是隐含狄利克雷分布（LDA）。当然，本文的动态主题模型也是主题模型的一种，不过为了方便理解，我们还是来回顾一下LDA。

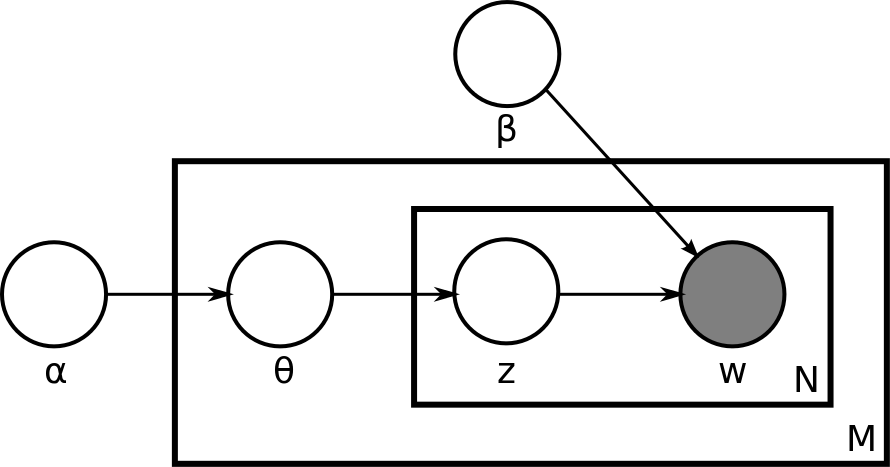
来自：https://en.wikipedia.org/wiki/Latent_Dirichlet_allocation
来自：https://en.wikipedia.org/wiki/Latent_Dirichlet_allocation

我们定义：

α 是狄利克雷先验的参数，是每个文档可能的主题分布。

\theta _{m}，当α 落实到一个文档m，\theta _{m}是文档m的主题模型。而且α代表的是狄利克雷分布，\theta _{m}代表的是多项式分布。 α很明显是\theta _{m}的共轭先验。

β 是狄利克雷先验的参数，但是，它是每个主题可能的文字分布。

{\displaystyle z_{mn}} 是在文档m中，第n个文字的主题。 继续阅读卡内基梅隆大学（CMU），那些经受住时间考验的机器学习论文–第二弹：动态主题模型

卡内基梅隆大学（CMU），那些经受住时间考验的机器学习论文–第一弹：互联网拓扑规律研究

这一期，接着上一期，开始我们的卡内基梅隆大学（CMU）机器学习论文之旅。

CMU果然是机器学习的牛叉大学（拥有专门的机器学习专业系）。David 9翻看所有获得“Test of Time Award”（经得住时间考验奖）的论文，没有一篇论文是应用型，全部是奠基类的基础研究文章，不得不赞叹才疏学浅啊。先来获奖看一下列表：

  1. Graphs over time: densification laws, shrinking diameters and possible explanations [.pdf]
    Jure Leskovec, Jon Kleinberg, Christos Faloutsos, Test of Time Award, KDD 2016
  2. Dynamic Topic Models [.pdf]
    John Lafferty, David Blei, Test of Time Award, ICML 2016
  3. Realistic, Mathematically Tractable Graph Generation and Evolution, Using Krinecker Multiplication [.pdf]Jure Leskovec, Deepayan Chakrabarti, Jon M. Kleinberg, Christos Faloutsos, Test of Time Award, ECML/PKDD 2015
  4. Beyond Independent Relevance: Methods and Evaluation Metrics for Subtopic Retrieval [.pdf]
    Cheng Zhai, William Cohen, John Lafferty, Test of Time Award, SIGIR 2014
  5. Diffusion Kernels on Graphs and Other Discrete Input Spaces [.pdf]Risi Kondar and John Lafferty, Test of Time Award, ICML 2012
  6. Conditional Random Fields: Probabilistic Models for Segmenting and Labeling Sequence Data [.pdf]
    John Lafferty, Andrew McCallum, and Fernando C. N. Pereira, Test of Time Award, ICML 2011
  7. On Power-Law Relationships of the Internet Topology [.pdf]Michalis Faloutsos, Petros Faloutsos and Christos Faloutsos, Test of Time Award, ACM SIGCOMM 2010
  8. Integration of heterogeneous databases without common domains using queries based on textual similarity [.pdf]William Cohen, Test of Time Award, ACM SIGMOD, 2008

David 9发现一个规律，里面几乎所有论文都和“图”有关系啊，看来CMU对Graph研究很热衷啊？ 继续阅读卡内基梅隆大学（CMU），那些经受住时间考验的机器学习论文–第一弹：互联网拓扑规律研究

#12 机器学习能力自测题—看看你的机器学习知识能打几分？不容错过的机器学习试题与术语

一直苦于没有办法自测一下机器学习知识掌握程度，最近看到一篇Ankit Gupta写的博客：Solutions for Skilltest Machine Learning : Revealed。有40题机器学习自测题，马上可以看看你的机器学习知识能打几分？顺便还能查漏补缺相关术语，以及SVM, 隐马尔科夫, 特征选择, 神经网络, 线性回归等众多知识点.

以下是试题, 附答案：

Q1：在一个n维的空间中， 最好的检测outlier(离群点)的方法是：

A. 作正态分布概率图

B. 作盒形图

C. 马氏距离

D. 作散点图

答案：C

马氏距离是基于卡方分布的，度量多元outlier离群点的统计方法。更多请详见：这里和”各种距离“。

 

Q2：对数几率回归（logistics regression）和一般回归分析有什么区别？： 继续阅读#12 机器学习能力自测题—看看你的机器学习知识能打几分？不容错过的机器学习试题与术语