涉及领域不多的机器学习爱好者经常会把IoU，ROI 和 ROC，AUC 这样的评价函数（Metric functions）搞混。其实记住它们也没那么难，David 9今天就来帮大家理一理：
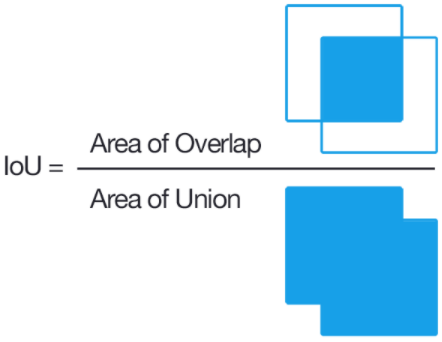
1. IoU (Intersection over Union)，交集并集比
2. ROI (region of interest) , 感兴趣区域
3. ROC (Receiver Operating Characteristic curve) 受试者工作特征曲线
4. AUC (Area Under the Curve) ， 曲线下区域
首先要区分，前两个是目标检测领域的术语；后两个是从医疗领域引进的，但是所有机器学习准确率都可能用到该指标。
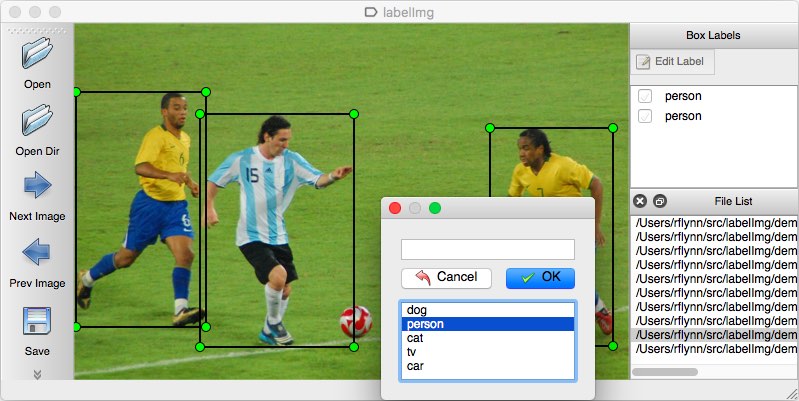
最容易理解的是第2个ROI，我们做任何目标检测在准备数据集时都要选择感兴趣区域, 我们之前的文章也提到过：
labelImg 就是一个不错的标注工具。帮助你选择目标检测的感兴趣框。是的这不是一个评价函数，是一个概念而已。 继续阅读做机器学习，再别把IoU，ROI 和 ROC，AUC 搞混了 ！聊聊目标检测，医疗领域的那些评价函数
虽然ICLR2018将在今年5月召开，但是双盲评审已经如火如荼。目前评审结果排位第一的论文试图解决神经网络在预测分布上缺乏鲁棒性的问题。
我们都知道神经网络和人一样也有判断“盲点”。早在2015年Ian Goodfellow 就提出了攻击神经网络的简单方式，把cost函数 J（θ, x, y）对输入图片x求导，得到一个对神经网络来说loss下降最快的干扰噪声：
一旦加入这个细微噪声（乘以0.007），图片的分错率就达到了99.3% ！
这种生成对抗样本的攻击方法被称为FGM（fast-gradient method快速梯度法），当然还有许多攻击方法, 下面是对数字8的测试攻击样例:
有了攻击方法我们就能增加神经网络的鲁棒性, 那么FGM是加强模型鲁棒性的最好参考吗？
该论文的答案是：NO ！
论文提出了Wasserstein鲁棒更新方法WRM，文章指出，通过WRM训练出的模型有更鲁棒的训练边界，下面是David 9最喜欢的论文实验图：
杰出的论文不仅应该有实用的方法，更应该有让人豁然开朗的理论，不是吗？
上图Figure 1是一个研究分类边界的人工实验，蓝色的样本点和红色的样本点是两类均匀样本，因为蓝色样本比红色样本多得多，所以分类边界倾向于向“外”推。 继续阅读ICLR2018抢先看！深挖对抗训练：提高模型预测分布的鲁棒性, Wasserstein鲁棒更新方法WRM，以及Earth Mover’s Distance
如果AI的本质是在可接受时间内搜索到最优解，那么容易定义最优解的问题都是AI可以解决的。这样，人类的“情感”看起来如此“珍贵”，因为它很难用人工定义“最优解” — David 9
相信大家还记得2017年初人工智能Libratus完胜德州扑克顶级玩家的事，年底卡耐基梅隆大学（CMU）在NIPS 2017上公开这一贡献并获得最佳论文奖。这一进展之所以让人兴奋，是因为它为不完美信息博弈（Imperfect-Information Games）问题提供了新的解决思路：
像棋类游戏，双方都是共享一切信息的，这种博弈称为完美信息博弈。而扑克类，谈判，商业决策等类似问题，双方的信息都是不公开给对方的，这就提高了AI算法搜索最优解的难度。
对于完美信息博弈，每一步Action引出下一步子状态，接下来在子状态中求解最优解即可：
对于不完美信息博弈，我们不能安心地解决眼前的子问题，因为我们同时必须考虑：“对手的手牌现在会是什么样的？”，“他下一次会用什么策略？”等等烦人的问题，因此许多平行的子问题是我们必须同时考虑的：
继续阅读德州扑克AI(Libratus)的背后：不完美信息博弈中，求解安全嵌套的子博弈, #NIPS 2017最佳论文奖
