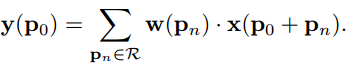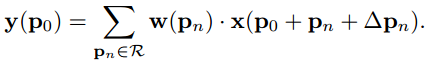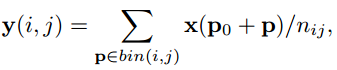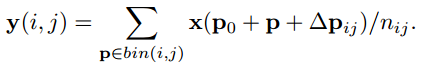MSRA微软亚洲研究院 最新卷积网络: Deformable Convolutional Networks(可变形卷积网络)

抽样方法的改进似乎像人类进化一样永无休止 — David 9

CVPR 2017机器视觉顶会今年6月21号才举办，但是2016年11月就投稿截止了。微软每年都是CVPR大户，今天我们要讲解的就是MSRA微软亚洲研究院的最新投稿论文：Deformable Convolutional Networks。（很可能被收录哦~）我们暂且翻译为：可变形卷积网络。

这是一种对传统方块卷积的改进核。本质是一种抽样改进。

谈到抽样，人脑好像天生知道如何抽样获得有用特征，而现代机器学习就像婴儿一样蹒跚学步。我们学会用cnn自动提取有用特征，却不知用什么样的卷积才是最有效的。我们习惯于方块卷积核窗口，而Jifeng Dai的work认为方块不是最好的形状：

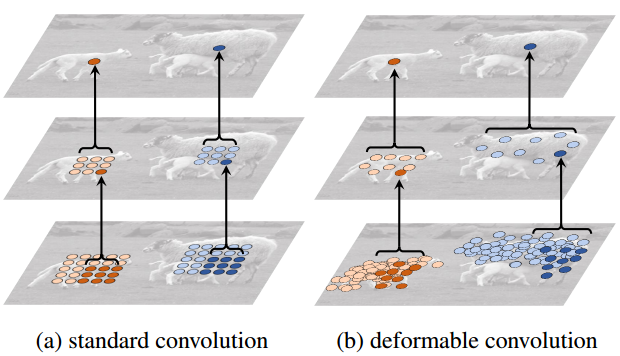
如果能让网络自己学习卷积窗口形状，是不是一件很美好的事情？上图是用方块卷积和可变形卷积的比较。如果用方块卷积无法高效率地收集到绵羊的特征像素点，而可变形卷积尝试收集到那些最有用的像素点。

可变形卷积为每个卷积采样点加上一个偏移量来达到更好的采样效果：

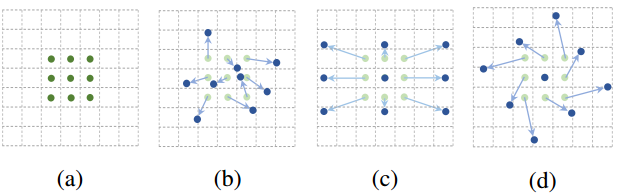
以9个像素点的卷积窗口为例，只要为每个像素点加上一个偏移向量（上图 (b) (c) (d)），就可做到卷积窗口的可变形。

很显然，传统卷积窗口只要训练每个卷积窗口的像素权重参数即可。而可变形卷积网络必须外加一些参数用来训练卷积窗口的形状（各个像素的偏移向量offset）：

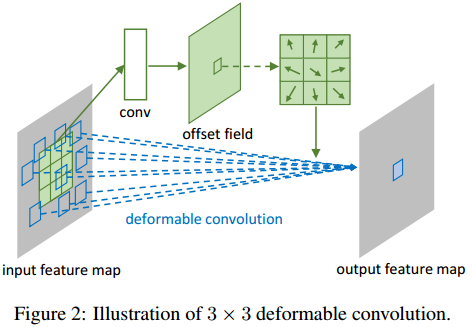
上图的offset field就是变形卷积外加的待训练参数，大小和输入层图片大小一样（input feature map），卷积窗口在offset field上滑动就呈现了卷积像素偏移的效果，达到采样点优化的效果。

对于传统的卷积窗口偏移向量是这样的：

典型的9点的方格，中间向8个方向偏移8个点。传统的卷积输出是这样获得的：

卷积窗口中的每个像素点pn有权重w，p0是代表窗口输出的每个像素点 
。x是输入层像素点集合。如对方格变形偏移，只需加上Δpn：

注意到Δpn只是影响x输入层像素的抽样，并不影响窗口像素权重w。

所以总结我们有两组参数需要训练：w 和 Δpn。

对于可变形的ROI感兴趣区域池化，也是同样的变形方式。

传统ROI，把任意大小的区域转化成固定大小bin的特征图：

p0是ROI左上角的点，nij （i 行，j 列）是固定大小bin里的总像素数。如对ROI进行可变形操作：

依然是对每个输出像素加一个偏移量Δpij，也就是下图中多加入的的fc 层：

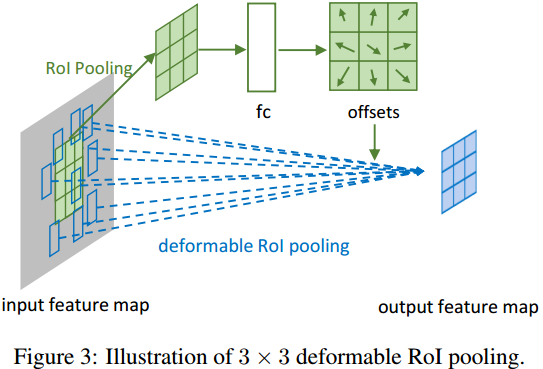
接下来，看一下实验的可视化效果：

从左到右，是可变形卷积网络从低层到高层的卷积窗口采样的像素点。中间那个绿点是不动的中心点（无偏移向量）。是不是很好地找到了偏移向量覆盖特征？

下面图片是可变形卷积使用在ROI池化中的窗口偏移选择：

最后我们看一下实验结果如何：

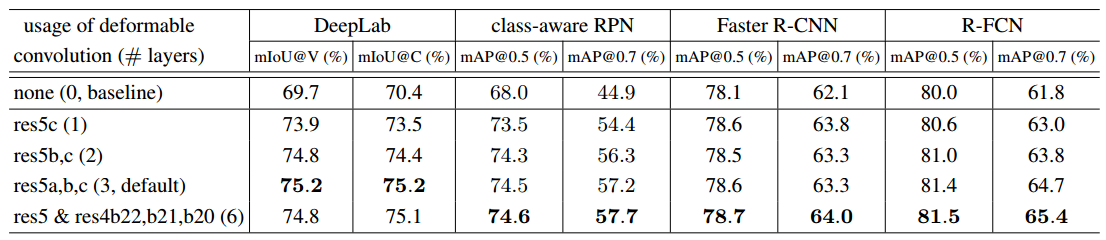
上图是在ResNet-101网络结构上， 对class-aware RPN, Faster R-CNN, and R-FCN等一系列目标检测算法的改进。第一行（none(0, baseline)）是没有任何改进的效果。第二行res5c(1)是在倒数第1层卷积上用可变形卷积的效果（3*3的核）。以此类推，res5a,b,c(3, default)是在倒数第3层上使用可变形卷积的效果（似乎较好？）。

这篇论文的相关工作写的很详尽，应该是和Spatial Transform Networks (STN) 殊途同归，如感兴趣详情请见原论文。

 

参考文献：

1. https://arxiv.org/pdf/1703.06211.pdf
2. https://zh.wikipedia.org/wiki/ArXiv
3. https://www.zhihu.com/question/57493889
4. https://github.com/felixlaumon/deform-conv
5. https://github.com/oeway/pytorch-deform-conv
6. http://baike.baidu.com/item/ROI/1125333
7. https://en.wikipedia.org/wiki/Region_of_interest
8. https://www.zhihu.com/question/35887527

本文章属于“David 9的博客”原创，如需转载，请联系微信: david9ml，或邮箱：yanchao727@gmail.com

或直接扫二维码: