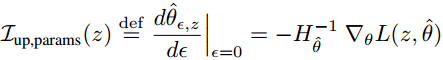ICML 2017论文精选#1 用影响函数(Influence Functions)理解机器学习中的黑盒预测（Best paper award 最佳论文奖@斯坦福）

无论是机器学习还是人类学习，似乎一个永恒的问题摆在外部指导者的面前：“我究竟做错了什么使得它（他）的学习效果不理想？” — David 9

之前我们提到过，端到端学习是未来机器学习的重要趋势。

可以想象在不久的将来，一切机器学习模型可以精妙到酷似一个“黑盒”，大多数情况下，用户不再需要辛苦地调整超参数，选择损失函数，尝试各种模型架构，而是像老师指导学生一样，越来越关注这样一个问题：我究竟做错了什么使得它的学习效果不理想？是我的训练数据哪里给的不对？

今年来自斯坦福的ICML最佳论文正是围绕这一主题，用影响函数（influence functions）来理解机器模型这一“黑盒”的行为，洞察每个训练样本对模型预测结果的影响。

文章开篇结合影响函数给出单个训练样本 z 对所有模型参数 θ 的影响程度 I 的计算:

其中 ε 是样本 z 相对于其他训练样本的权重, 如果有 n 个样本就可以理解为 1/n 。

是Hessian二阶偏导矩阵, 蕴含所有训练样本(总共 n 个)对模型参数θ 的影响情况.

而梯度

蕴含单个训练样本 z 对模型参数 θ 的影响大小.

L : 即训练样本的损失.

所以总结影响指数 I 主要由2部分信息: 

1. Hessian矩阵蕴含的其他训练样本的影响信息.
2. 当前训练样本 z 对被模型参数 θ 的影响信息.

文章进一步给出单个训练样本 z 对单个测试样本 Ztest 预测结果的影响程度 I 的计算:

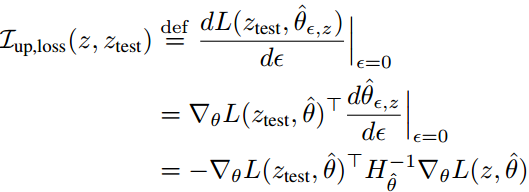可以总结影响程度 I 现在主要由3部分信息(分别对应式子中的三项): 

1. 当前测试样本 ztest 被模型参数 θ 的影响信息
2. Hessian矩阵蕴含的其他训练样本的影响信息
3. 当前训练样本 z 对被模型参数 θ 的影响信息

这个式子较上一个式子的不同在于第1个信息, 即测试样本被模型参数 θ 影响的程度.

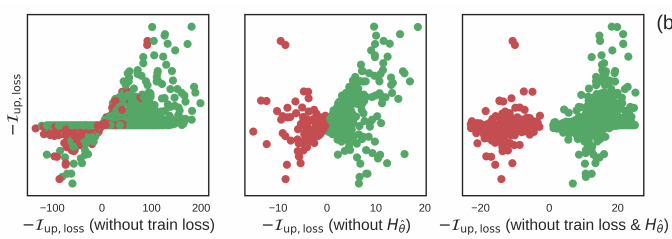
让我们看看如果缺少式子中的项会发生什么:

如果没有第3项单个样本z的损失值信息, 就会像上图最左的图片, 单个样本z的影响程度I就会出现偏差.

如果没有第2项Hessian矩阵, 缺少了其他训练样本的参照, 和测试样本同标签的训练样本(绿色样本)只会对预测测试样本产生正作用, 相反, 如果测试样本不同标签的训练样本(红色样本)只会对预测测试样本产生负作用.
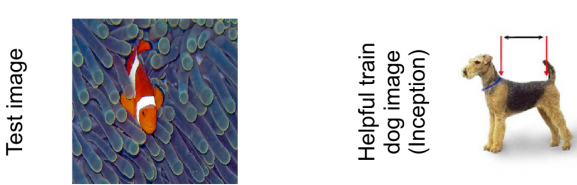
这是不符合事实的, 因为有些训练样本和测试样本虽然是同标签的, 但是对训练是有负作用的, 下图右侧的7是训练样本, 但是它是扰乱训练的训练样本:

即: 如果多了右侧的7 这个训练样本, 更有可能导致左侧的测试样本判别出错(损失值变大).

通过观察训练样本，提供这样一个高效的影响程度计算，对于未来学者开发新模型，理解模型行为和诊断模型，都有很大帮助。

文章末尾给出了几个影响函数的实际应用案例（use cases）。

1.  理解模型的行为：

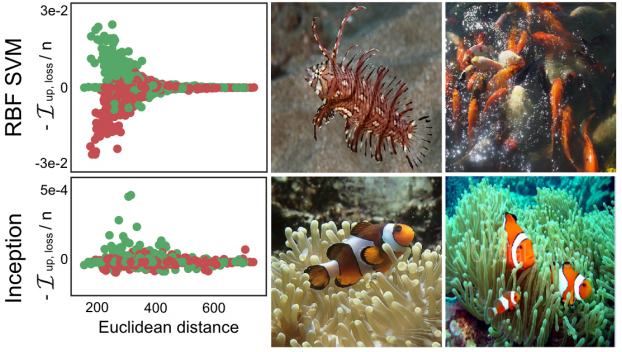
文章给出了用影响函数比较支持向量机（SVM）和深度网络（Inception）的一个生动例子，一个用来识别“鱼”和“狗”的模型：

绿色的点是标签为“鱼”的训练样本，红色的点是标签为“狗”的训练样本。

主要SVM和Inception点图的比较，横坐标是训练样本与测试样本的欧几里得距离（可以理解为图片相似度），纵坐标是该训练样本对单个测试样本的影响程度。

有意思的是：

1. 在SVM模型中，对于那些与测试样本相差很多的训练样本（欧几里得距离较大），对于模型判别测试样本几乎不起作用（I几乎等于0）。这正是符合了SVM的支持向量在判别中的重要作用。（越是难以判别的训练样本，对模型影响越大）

2. 在Inception深度网络中，无论欧式距离多大，一个训练样本都会对测试样本的判断产生影响。 这一点证明了深度网络的优势，每一个训练样本都可能对模型优化产生作用（无论是正样本还是负样本）

3. 右侧的两张样图是训练样本中对预测影响最大的样图，可以看到，SVM中两张最不像“鱼”的样本，反而对模型判别起到较大作用 ，而Inception中得两张“鱼”图就比较正常。

2.  生成对抗样本：

有了对于单个训练样本的影响函数，我们可以生成对抗训练样本，找出模型的“弱点”：

如上图，我们可以借助影响函数构造影响程度较大训练样本（其实这个样本很原来的训练样本差别并不大），让模型的预测值发生巨变（甚至导致分类错误）。

3.  评估训练样本集的价值：

如果训练样本集和测试样本集不是同一个域或者说不是同一个分布，即使收集再多的训练样本，对于训练模型也是没有帮助的。

如果计算影响程度I 时，只有极少部分的训练样本对测试样本的预测有影响时，你要小心了，可能你训练样本收集的域不正确，你需要尝试换种方式收集训练样本。

4.  找出被标记错的训练样本：

影响函数还可以用来检测那些被标记错的训练样本，如果极少数训练样本的预测程度相对过大，你就要考虑是否这些样本其实就是被标记错了？：

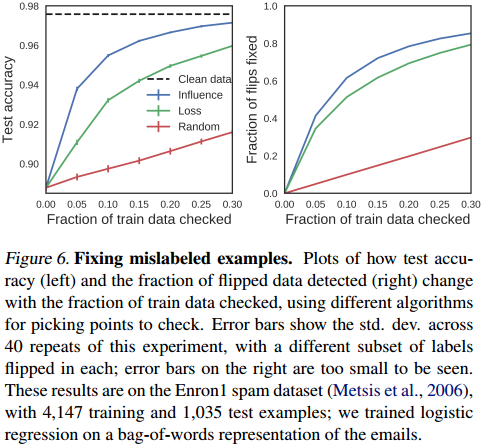
上图展示了训练数据集中的一部分训练样本被评估后的效果，对预测准确率的提高是有一些帮助的（特别是你确定有一些训练样本被标记错类别了）。

这就是今天David 9的分享，不得不说David 9很喜欢ICML中的文章，多数都很普世有深度，希望大家对我上面的见解提出指正，也许有些分析会有问题。

 

参考文献：

1. http://proceedings.mlr.press/v70/koh17a/koh17a.pdf
2. https://arxiv.org/abs/1608.06993https://en.wikipedia.org/wiki/Hessian_matrix
3. https://github.com/kohpangwei/influence-release

本文采用署名 – 非商业性使用 – 禁止演绎 3.0 中国大陆许可协议进行许可。著作权属于“David 9的博客”原创，如需转载，请联系微信: david9ml，或邮箱：yanchao727@gmail.com

或直接扫二维码: