ICLR 2017论文精选#1之颠覆三观—理解深度学习要重新审视泛化能力（Best paper award 最佳论文奖）

我似乎看到了一个未来: 机器自身不断生成全新的模型架构, 去应对各种未知的问题. —— David 9

最近是个躁动的时节(ICLR 2017, Google I/O , Openstack峰会, 微软Build 等等), David 9也有点忙晚更了, 大家见谅. 今天, 接着拿ICLR 2017的一篇最佳论文, 这篇毁三观的论文实在是忍不住要拿出来讲一下. 论文来自Google 大脑团队:

是不是看到了我们熟悉的Bengio? 但是 第一作者是MIT的实习生哦~ 是的, 其实这篇论文理论并不艰深, 亮点是实验方法和颠覆三观的结论. 探讨的是机器学习界古老的话题: 泛化能力.
提到模型泛化能力, 人们一般的观念是VC维, 也就是模型越复杂(训练参数越多), 模型的泛化能力越差. 该文章用深度学习模型实验指出了这种错误观念, 事实上, 深度学习模型随着模型参数的增加, 模型依然具有一定泛化能力:

如上图, 对于一些经典深度学习网络, 我们用平均每个样本带有训练参数的数量来评价模型的复杂度,可以看到, “大岩蛇”resnet复杂度最高, 但事实上它在同样情况下的泛化能力是最高的, 即测试错误率是最低的. 这与VC维认为复杂度高就泛化能力越低的论调是违背的.

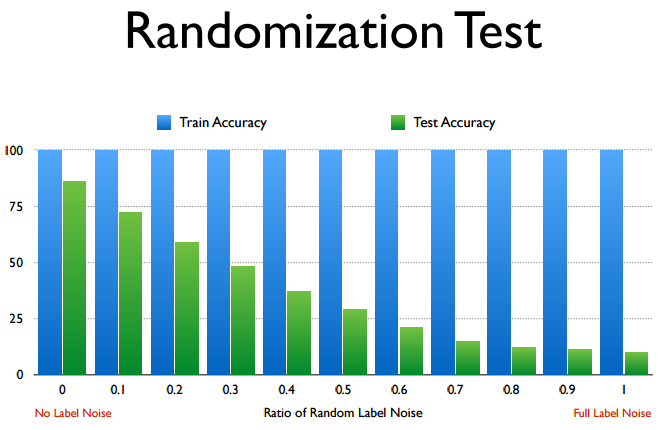
文章对一些经典深度学习网络做了随机样本实验:

把样本是实际label随机打乱后, 就是一个杂乱无章的数据集, 依旧用原来的深度网络训练结果如下:

横坐标是”打乱”的程度,  纵坐标是训练误差和测试误差. 令人惊讶的是, 即使是完全打乱, 神经网络依然能够在训练一定时间后收敛, 而且有一定的泛化能力(绿色轴). 

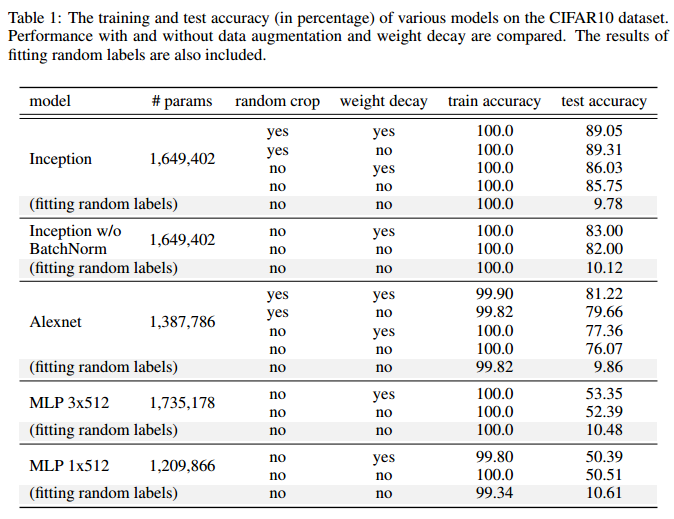
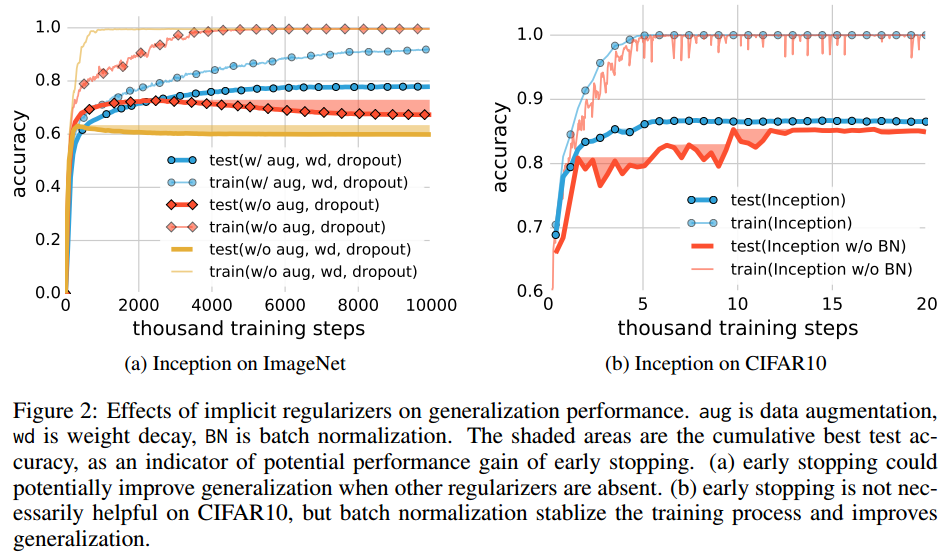
深度网络似乎自带泛化能力, 但这种泛化能力来自哪里? 是因为现代深度网络加了很多抵制过拟合的Tricks吗? 就是那些L2正则项, Dropout, 训练步长衰减, batch normalization 等等的影响吗? 文章实验给出的答案是否定的 ! 文章认为:

类似Dropout, Batch normalization这样的显式或隐式正则方法, 在模型中可以增强泛化能力, 但不是必要的 !

因为实验证明 , 不用任何显式或隐式的正则化方法, 模型依然自带一定的泛化能力: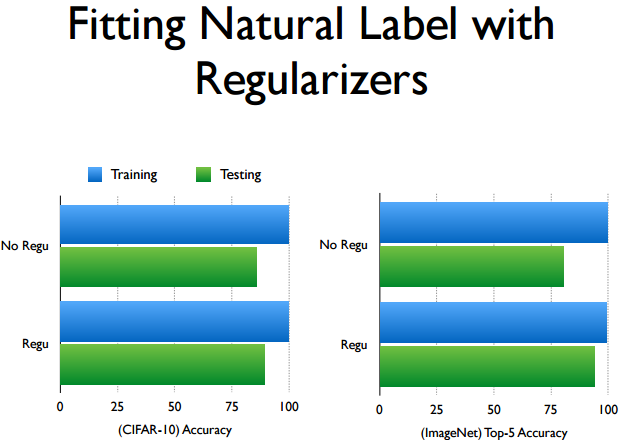

那么究竟这种深度学习自带的泛化能力来自哪里?

我们知道, 对于集成学习, 如Adaboost, 随机森林, 也是自带高于随机猜测的泛化能力, 但是它们自带的泛化能力似乎就是没有深度学习架构的模型来的强, 这又是为什么?

这篇论文给了我们一些启迪. 事实上, 有一些更隐性的正则化方法是我们平时并不注意的, 比如深度学习中我们习惯了使用SGD作为优化器去优化网络, SGD在一定程度上可以帮助网络收敛到一个较好的正则范围内(只是你不太察觉).

在深度学习网络中, 训练参数非常之多(上百万已经是少量的了), SGD优化器的优化是那么容易, 以至于在随机数据上都能训练收敛. 剩下的事情, 只需要收敛到一个较好的范围就可以了. 而SGD碰巧搭配深度学习的框架, 可以收敛到一个较好的范围. 这就是泛化能力的真实来源. David 9 的理解是:

模型容易训练和收敛, 与泛化能力没有必然关系. 泛化能力是模型架构和优化方法的综合,当这两个因素确定下来后, 其他形式的正则对于实际泛化能力的提高帮助并不是太大. 有朝一日, 我们会理解目前深度学习网络的局限, 从而催生新的模型架构. 

总的来说, 这篇文章很有”抛砖引玉”的作用, 为以后学者设计新型模型, 甚至超越深度学习的架构模型提供了思路和参考.

参考文献：

  1. ICLR 2017 被接受论文列表
  2. UNDERSTANDING DEEP LEARNING REQUIRES RETHINKING GENERALIZATION
  3. http://www.iclr.cc/lib/exe/fetch.php?media=iclr2017:czhang_iclr2017.pdf
  4. http://www.iclr.cc/doku.php?id=iclr2017:schedule
  5. https://research.googleblog.com/2017/04/research-at-google-and-iclr-2017.html

本文章属于“David 9的博客”原创，如需转载，请联系微信: david9ml，或邮箱：yanchao727@gmail.com

或直接扫二维码:

发布者

David 9

邮箱：yanchao727@gmail.com 微信: david9ml

发表回复

您的电子邮箱地址不会被公开。 必填项已用 * 标注