DeepMind新型神经网络：可异步训练的深度网络！— “解耦神经网络” 与 “合成梯度”

如果深度学习不是神经网络的终点， 那么神经网络会跟随人类进化多久？ — David 9

自3年前Google收购DeepMind，这家来自英国伦敦的人工智能公司就一直站在神经网络与深度学习创新的风口浪尖（AlphaGo，DeepMind Health）。

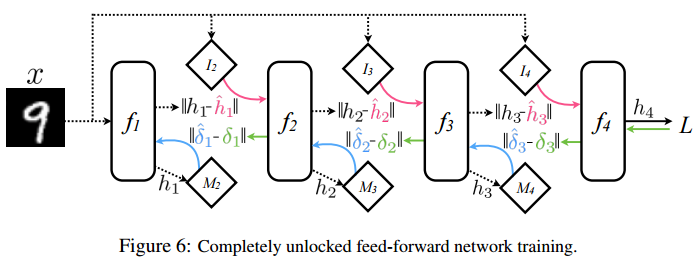
今天要介绍的“解耦神经网络接口”（Decoupled Neural Interfaces）的异步网络，就是出自DeepMind之手。这篇2016发表的论文试图打破传统的前向传播和后向传播按部就班的训练过程。在传统神经网络, 整个过程是非异步的更新，更新也是逐层紧耦合的（图b）：

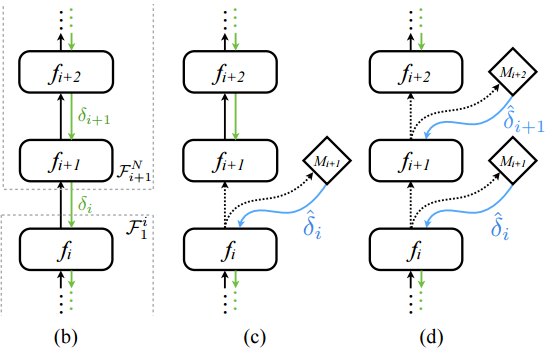
图(b)是传统普通前馈反馈神经网络（黑色是前馈箭头，绿色是反馈箭头），fi 层到fi+1 层的权重矩阵由fi+1层的偏导反馈δi 更新， 众所周知，反馈δi 必须等到后向反馈从输出层传递到fi+1 层后才能计算出。

为了试图解除这种“锁”（强耦合）(图(c)(d))，在(c)图中我们注意到在fi 层和fi+1 层之间，引入了模型Mi+1（图中菱形），又称人工“合成梯度”模型，用来模拟当前需要的梯度反馈更新。

有意思的是，模型Mi+1本身也可设计为神经网络。可以训练用来预测当前fi层和fi+1层之间需要的反馈更新δi，像这样：

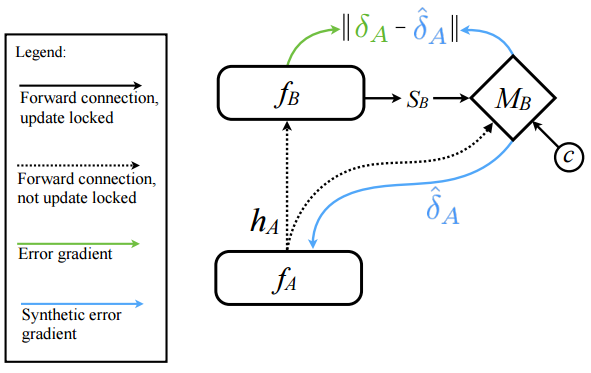
模型MB 的输出是后向反馈更新的估计（或者说模拟）：

模型MB 的输入是(hA, SB, c )。

其中hA代表fA层发出的信号（可以理解为前向传播信号），SB是上层 fB的状态，c是一些其他影响δA 的因素。随着真实的反馈和模型反馈的更新学习：

模型MB 对于权值更新的预测越来越准确。直到MB可以直接替代传统反向反馈的权值更新。

这就是“解耦神经网络” 与 “合成梯度”的简单原理。好似用一个“缓存” 瞬间提供需要的梯度下降！

接下来，我们看一下整个解耦神经网络异步训练的步骤究竟是怎样的：

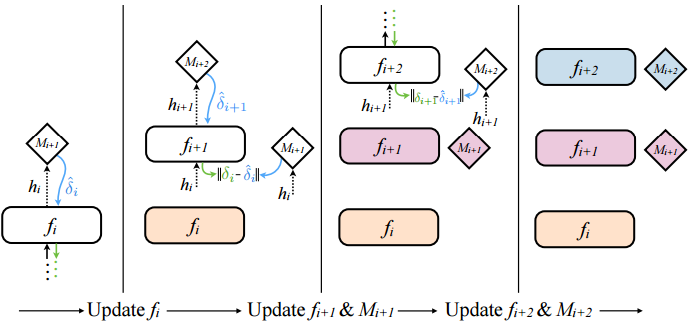
上图空白的方框是尚未更新的层，有颜色的框是已更新的层，从左到右是更新的步骤。可见：

1. 每一层的参数无需等待上一层的反馈过来才能更新，而是只要根据“合成梯度” Mi+1 直接更新。
2. 前向传播时，每一层的训练外加了一个步骤，即，这一层“合成梯度” Mi+1 的更新，随本层参数的更新一同更新。

这样的解耦神经网络训练效果如何？

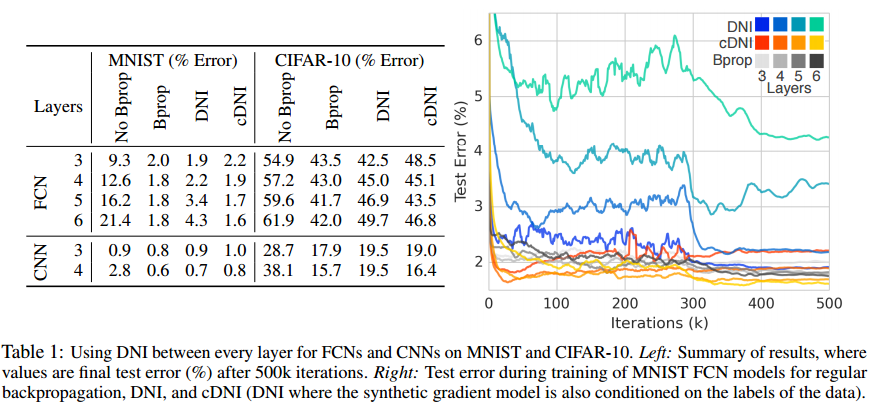
上图是DNI (论文提出的架构叫Decoupled Neural Interfaces),  cDNI(在”合成梯度”模型中还加入样本标签信息的算法),  以及一些传统后向传播算法(Bprop)的比较.

至少我们可有以下几点结论:

1. 在“合成梯度”模型中加入样本标签信息，对DNI泛函能力有较好的提高。
2. DNI需要充分迭代，大概大于300次迭代才能有较好效果。
3. 对于FCN，CNN都能改造成解耦网络，所以解耦网络较为容易扩展和推广。

甚至DeepMind给出了更通用的“全解耦”网络：

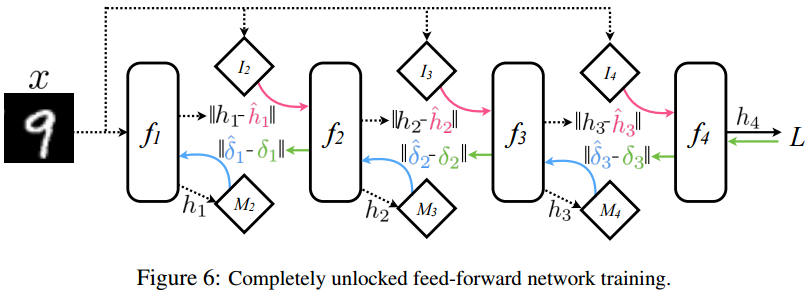
为所有的梯度传递（无论是前向的还是后向的）都增加一个“合成梯度”模型（图中菱形）来模拟需要的梯度下降。

这就是David 9对于“解耦神经网络” 与 “合成梯度”的解读。如果您想继续深入研究，请阅读原论文。如果你对实现解耦神经网络感兴趣，David9 下面为大家准备了一个摘自https://iamtrask.github.io/2017/03/21/synthetic-gradients/ 的简单实现，供大家参考：

这是一个输入（24位“01”串），预测输出（12位“01”串）的简单的解耦网络。

其中DNI类包装了用简单线性模型去模拟 “合成梯度”模型的方法。

decoupled_network.py 模拟解耦神经网络：

import numpy as np
import sys

def generate_dataset(output_dim = 8,num_examples=1000):
    def int2vec(x,dim=output_dim):
        out = np.zeros(dim)
        binrep = np.array(list(np.binary_repr(x))).astype('int')
        out[-len(binrep):] = binrep
        return out

    x_left_int = (np.random.rand(num_examples) * 2**(output_dim - 1)).astype('int')
    x_right_int = (np.random.rand(num_examples) * 2**(output_dim - 1)).astype('int')
    y_int = x_left_int + x_right_int

    x = list()
    for i in range(len(x_left_int)):
        x.append(np.concatenate((int2vec(x_left_int[i]),int2vec(x_right_int[i]))))

    y = list()
    for i in range(len(y_int)):
        y.append(int2vec(y_int[i]))

    x = np.array(x)
    y = np.array(y)

    return (x,y)

def sigmoid(x):
    return 1 / (1 + np.exp(-x))

def sigmoid_out2deriv(out):
    return out * (1 - out)

class DNI(object):

    def __init__(self,input_dim, output_dim,nonlin,nonlin_deriv,alpha = 0.1):

        self.weights = (np.random.randn(input_dim, output_dim) * 2) - 1
        self.bias = (np.random.randn(output_dim) * 2) - 1

        self.weights_0_1_synthetic_grads = (np.random.randn(output_dim,output_dim) * .0) - .0
        self.bias_0_1_synthetic_grads = (np.random.randn(output_dim) * .0) - .0

        self.nonlin = nonlin
        self.nonlin_deriv = nonlin_deriv
        self.alpha = alpha

    def forward_and_synthetic_update(self,input,update=True):

        self.input = input
        self.output = self.nonlin(self.input.dot(self.weights)  + self.bias)

        if(not update):
            return self.output
        else:
            self.synthetic_gradient = (self.output.dot(self.weights_0_1_synthetic_grads) + self.bias_0_1_synthetic_grads)
            self.weight_synthetic_gradient = self.synthetic_gradient * self.nonlin_deriv(self.output)

            self.weights -= self.input.T.dot(self.weight_synthetic_gradient) * self.alpha
            self.bias -= np.average(self.weight_synthetic_gradient,axis=0) * self.alpha

        return self.weight_synthetic_gradient.dot(self.weights.T), self.output

    def normal_update(self,true_gradient):
        grad = true_gradient * self.nonlin_deriv(self.output)

        self.weights -= self.input.T.dot(grad) * self.alpha
        self.bias -= np.average(grad,axis=0) * self.alpha

        return grad.dot(self.weights.T)

    def update_synthetic_weights(self,true_gradient):
        self.synthetic_gradient_delta = (self.synthetic_gradient - true_gradient)
        self.weights_0_1_synthetic_grads -= self.output.T.dot(self.synthetic_gradient_delta) * self.alpha
        self.bias_0_1_synthetic_grads -= np.average(self.synthetic_gradient_delta,axis=0) * self.alpha

np.random.seed(1)

num_examples = 100
output_dim = 8
iterations = 100000

x,y = generate_dataset(num_examples=num_examples, output_dim = output_dim)

batch_size = 10
alpha = 0.01

input_dim = len(x[0])
layer_1_dim = 64
layer_2_dim = 32
output_dim = len(y[0])

layer_1 = DNI(input_dim,layer_1_dim,sigmoid,sigmoid_out2deriv,alpha)
layer_2 = DNI(layer_1_dim,layer_2_dim,sigmoid,sigmoid_out2deriv,alpha)
layer_3 = DNI(layer_2_dim, output_dim,sigmoid, sigmoid_out2deriv,alpha)

for iter in range(iterations):
    error = 0
    synthetic_error = 0

    for batch_i in range(int(len(x) / batch_size)):
        batch_x = x[(batch_i * batch_size):(batch_i+1)*batch_size]
        batch_y = y[(batch_i * batch_size):(batch_i+1)*batch_size]

        _, layer_1_out = layer_1.forward_and_synthetic_update(batch_x)
        layer_1_delta, layer_2_out = layer_2.forward_and_synthetic_update(layer_1_out)
        layer_3_out = layer_3.forward_and_synthetic_update(layer_2_out,False)

        layer_3_delta = layer_3_out - batch_y
        layer_2_delta = layer_3.normal_update(layer_3_delta)
        layer_2.update_synthetic_weights(layer_2_delta)
        layer_1.update_synthetic_weights(layer_1_delta)

        error += (np.sum(np.abs(layer_3_delta)))
        synthetic_error += (np.sum(np.abs(layer_2_delta - layer_2.synthetic_gradient)))
    if(iter % 100 == 99):
        sys.stdout.write("\rIter:" + str(iter) + " Loss:" + str(error) + " Synthetic Loss:" + str(synthetic_error))
    if(iter % 10000 == 9999):
        print("")

参考文献：

1. https://iamtrask.github.io/2017/03/21/synthetic-gradients/
2. Decoupled Neural Interfaces using Synthetic Gradients

本文章属于“David 9的博客”原创，如需转载，请联系微信: david9ml，或邮箱：yanchao727@gmail.com

或直接扫二维码: