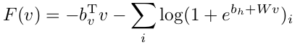前言:
本文主要是bengio的deep learning tutorial教程主页中最后一个sample:rnn-rbm in polyphonic music. 即用RNN-RBM来model复调音乐,训练过程中采用的是midi格式的音频文件,接着用建好的model来产生复调音乐。对音乐建模的难点在与每首乐曲中帧间是高度时间相关的(这样样本的维度会很高),用普通的网络模型是不能搞定的(普通设计网络模型没有考虑时间维度,图模型中的HMM有这方面的能力),这种情况下可以采用RNN来处理,这里的RNN为recurrent neural network中文为循环神经网络,另外还有一种RNN为recursive neural network翻为递归神经网络。本文中指的是循环神经网络。
RNN简单介绍:
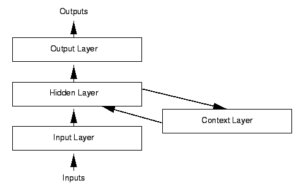
首先来看RNN和普通的feed-forward网络有什么不同。RNN的网络框架如下:
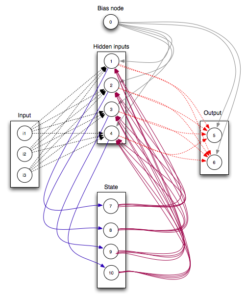
由结构图可以知道,RNN和feed-forward相比只是中间隐含层多了一个循环的圈而已,这个圈表示上一次隐含层的输出作为这一次隐含层的输入,当然此时的输入是需要乘以一个权值矩阵的,这样的话RNN模型参数只多了个权值矩阵。更形象的RNN图可以参考:
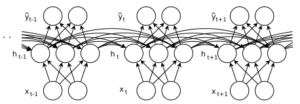
以及图:
按照上图所示,可知道RNN网络前向传播过程中满足下面的公式(参考文献Learning Recurrent Neural Networks with Hessian-Free Optimization):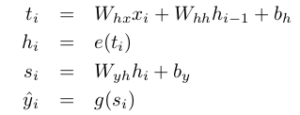
相信熟悉普通深究网络的同学看懂这些应该不难。
RNN-RBM简单介绍:
RNN-RBM来自ICML2012的论文:Modeling Temporal Dependencies in High-Dimensional Sequences: Application to Polyphonic Music Generation and Transcription,它由一个单层的RBM网络和单层的RNN网络构成,且由RNN网络的输出作为最终网络的输出。RBM部分当生成模型的功能,比如这里的音乐生成,RNN部分当判别模型作用,比如它的输出当值可当做提取的特征。RNN-RBM模型的结构如下:
模型上面是RBM部分,下面是RNN部分,对应的公式可以参考论文。模型中一共有9个参数:![]()
对该loss function求导,然后采用SGD算法就可以求出模型中的各个参数了。当然了,其中的RBM部分还需要用Gibbs采样完成CD-k算法。
实验结果:
实验部分参考http://deeplearning.net/tutorial/rnnrbm.html,实验须用的数据和paper对应的见http://www-etud.iro.umontreal.ca/~boulanni/icml2012. 由于本人对乐理方面的知识不是很懂,很多实验代码细节没有去深究,只是看下算法的大概流程。由RNN-RBM生成的两个pinao roll数据如下(程序跑了20个小时左右):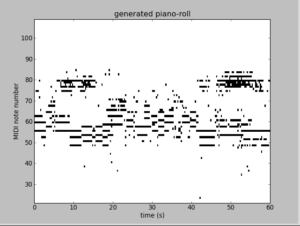
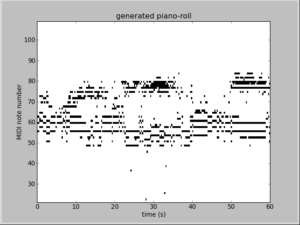
迭代200次后的cost为:
...... Epoch 197/200 -4.7050858655 Epoch 198/200 -4.69198161366 Epoch 199/200 -4.66586797348 Epoch 200/200 -4.68651185036
代码如下:
# Author: Nicolas Boulanger-Lewandowski
# University of Montreal (2012)
# RNN-RBM deep learning tutorial
# More information at http://deeplearning.net/tutorial/rnnrbm.html
import glob
import os
import sys
import numpy
try:
import pylab
except ImportError:
print "pylab isn't available, if you use their fonctionality, it will crash"
print "It can be installed with 'pip install -q Pillow'"
from midi.utils import midiread, midiwrite
import theano
import theano.tensor as T
from theano.tensor.shared_randomstreams import RandomStreams
#Don't use a python long as this don't work on 32 bits computers.
numpy.random.seed(0xbeef)
rng = RandomStreams(seed=numpy.random.randint(1 << 30))
theano.config.warn.subtensor_merge_bug = False
#给定rbm的3个参数w,bv,bh,输入端数据v,以及gibbs采用长度k
#返回的tuple元素依次是:v_samples(k次gibbs采用得到的输入端数据,01化后的),cost(rbm模型中的-log(v)),monitor(监控用变量),
#updates(保留每次迭代的中间过程,如果是shared变量的话)
def build_rbm(v, W, bv, bh, k):
'''Construct a k-step Gibbs chain starting at v for an RBM.
v : Theano vector or matrix
If a matrix, multiple chains will be run in parallel (batch).
W : Theano matrix
Weight matrix of the RBM.
bv : Theano vector
Visible bias vector of the RBM.
bh : Theano vector
Hidden bias vector of the RBM.
k : scalar or Theano scalar
Length of the Gibbs chain.
Return a (v_sample, cost, monitor, updates) tuple:
v_sample : Theano vector or matrix with the same shape as `v`
Corresponds to the generated sample(s).
cost : Theano scalar
Expression whose gradient with respect to W, bv, bh is the CD-k approximation
to the log-likelihood of `v` (training example) under the RBM.
The cost is averaged in the batch case.
monitor: Theano scalar
Pseudo log-likelihood (also averaged in the batch case).
updates: dictionary of Theano variable -> Theano variable
The `updates` object returned by scan.'''
def gibbs_step(v): #该函数功能是一次gibbs采样后得到的mean_v,v
mean_h = T.nnet.sigmoid(T.dot(v, W) + bh)
h = rng.binomial(size=mean_h.shape, n=1, p=mean_h, #产生二项分布,隐含层节点01化
dtype=theano.config.floatX)
mean_v = T.nnet.sigmoid(T.dot(h, W.T) + bv)
v = rng.binomial(size=mean_v.shape, n=1, p=mean_v, #反向传播,输入层节点也01化
dtype=theano.config.floatX)
return mean_v, v #一次Gibbs采样后输入层01化前后的值
#输入的是v,输出的是每一次Gibbs采样后的v构成的list,一共进行k次Gibbs采样
chain, updates = theano.scan(lambda v: gibbs_step(v)[1], outputs_info=[v],
n_steps=k) #updates里面装的是每次的输入值
v_sample = chain[-1] #k次Gibbs采样后输入端的值(01化过后的)
mean_v = gibbs_step(v_sample)[0] #再次Gibbs前进一次,得到没有01化的输入端数码,用于监控的变量
monitor = T.xlogx.xlogy0(v, mean_v) + T.xlogx.xlogy0(1 - v, 1 - mean_v)
monitor = monitor.sum() / v.shape[0]
def free_energy(v): #公式4,能量的计算公式
return -(v * bv).sum() - T.log(1 + T.exp(T.dot(v, W) + bh)).sum()
cost = (free_energy(v) - free_energy(v_sample)) / v.shape[0] #代价函数
return v_sample, cost, monitor, updates
def shared_normal(num_rows, num_cols, scale=1):
'''Initialize a matrix shared variable with normally distributed
elements.'''
return theano.shared(numpy.random.normal(
scale=scale, size=(num_rows, num_cols)).astype(theano.config.floatX))
def shared_zeros(*shape):
'''Initialize a vector shared variable with zero elements.'''
return theano.shared(numpy.zeros(shape, dtype=theano.config.floatX))
def build_rnnrbm(n_visible, n_hidden, n_hidden_recurrent):
'''Construct a symbolic RNN-RBM and initialize parameters.
n_visible : integer
Number of visible units.
n_hidden : integer
Number of hidden units of the conditional RBMs.
n_hidden_recurrent : integer
Number of hidden units of the RNN.
Return a (v, v_sample, cost, monitor, params, updates_train, v_t,
updates_generate) tuple:
v : Theano matrix
Symbolic variable holding an input sequence (used during training)
v_sample : Theano matrix
Symbolic variable holding the negative particles for CD log-likelihood
gradient estimation (used during training)
cost : Theano scalar
Expression whose gradient (considering v_sample constant) corresponds to the
LL gradient of the RNN-RBM (used during training)
monitor : Theano scalar
Frame-level pseudo-likelihood (useful for monitoring during training)
params : tuple of Theano shared variables
The parameters of the model to be optimized during training.
updates_train : dictionary of Theano variable -> Theano variable
Update object that should be passed to theano.function when compiling the
training function.
v_t : Theano matrix
Symbolic variable holding a generated sequence (used during sampling)
updates_generate : dictionary of Theano variable -> Theano variable
Update object that should be passed to theano.function when compiling the
generation function.'''
W = shared_normal(n_visible, n_hidden, 0.01)
bv = shared_zeros(n_visible)
bh = shared_zeros(n_hidden)
Wuh = shared_normal(n_hidden_recurrent, n_hidden, 0.0001)
Wuv = shared_normal(n_hidden_recurrent, n_visible, 0.0001)
Wvu = shared_normal(n_visible, n_hidden_recurrent, 0.0001)
Wuu = shared_normal(n_hidden_recurrent, n_hidden_recurrent, 0.0001)
bu = shared_zeros(n_hidden_recurrent)
params = W, bv, bh, Wuh, Wuv, Wvu, Wuu, bu # learned parameters as shared
# variables
v = T.matrix() # a training sequence
u0 = T.zeros((n_hidden_recurrent,)) # initial value for the RNN hidden
# units
# If `v_t` is given, deterministic recurrence to compute the variable
# biases bv_t, bh_t at each time step. If `v_t` is None, same recurrence
# but with a separate Gibbs chain at each time step to sample (generate)
# from the RNN-RBM. The resulting sample v_t is returned in order to be
# passed down to the sequence history.
# 如果给定t时刻的v和t-1时刻的u,那么返回t时刻的u,bv,bh,含有25次Gibbs采样过程
# 如果只给定t-1时刻的u(即没有t时刻的v),则表示的是由rbm来产生v了,所以这时候返回的是t时刻的v和u,以及
# 迭代过程中输入端的变换过程updates
def recurrence(v_t, u_tm1):
bv_t = bv + T.dot(u_tm1, Wuv)
bh_t = bh + T.dot(u_tm1, Wuh)
generate = v_t is None
if generate:
v_t, _, _, updates = build_rbm(T.zeros((n_visible,)), W, bv_t, #第一个参数应该是v,因此这里的v是0
bh_t, k=25)
u_t = T.tanh(bu + T.dot(v_t, Wvu) + T.dot(u_tm1, Wuu))
return ([v_t, u_t], updates) if generate else [u_t, bv_t, bh_t]
# For training, the deterministic recurrence is used to compute all the
# {bv_t, bh_t, 1 <= t <= T} given v. Conditional RBMs can then be trained
# in batches using those parameters.
(u_t, bv_t, bh_t), updates_train = theano.scan( #训练rbm过程的符号表达式(每次只包括25步的Gibbs采样)
lambda v_t, u_tm1, *_: recurrence(v_t, u_tm1),
sequences=v, outputs_info=[u0, None, None], non_sequences=params)
v_sample, cost, monitor, updates_rbm = build_rbm(v, W, bv_t[:], bh_t[:],
k=15)
updates_train.update(updates_rbm)
# symbolic loop for sequence generation
(v_t, u_t), updates_generate = theano.scan(
lambda u_tm1, *_: recurrence(None, u_tm1),#进行generate产生过程的符号表达式,迭代200次
outputs_info=[None, u0], non_sequences=params, n_steps=200)
return (v, v_sample, cost, monitor, params, updates_train, v_t, #cost在build_rbm()中产生
updates_generate)
class RnnRbm: #两个功能,训练RNN-RBM模型和用训练好的RNN-RBM模型来产生样本
'''Simple class to train an RNN-RBM from MIDI files and to generate sample
sequences.'''
def __init__(self, n_hidden=150, n_hidden_recurrent=100, lr=0.001,
r=(21, 109), dt=0.3):
'''Constructs and compiles Theano functions for training and sequence
generation.
n_hidden : integer
Number of hidden units of the conditional RBMs.
n_hidden_recurrent : integer
Number of hidden units of the RNN.
lr : float
Learning rate
r : (integer, integer) tuple
Specifies the pitch range of the piano-roll in MIDI note numbers, including
r[0] but not r[1], such that r[1]-r[0] is the number of visible units of the
RBM at a given time step. The default (21, 109) corresponds to the full range
of piano (88 notes).
dt : float
Sampling period when converting the MIDI files into piano-rolls, or
equivalently the time difference between consecutive time steps.'''
self.r = r
self.dt = dt
(v, v_sample, cost, monitor, params, updates_train, v_t,
updates_generate) = build_rnnrbm(r[1] - r[0], n_hidden, #在该函数里面有设置迭代次数等参数
n_hidden_recurrent)
gradient = T.grad(cost, params, consider_constant=[v_sample])
updates_train.update(((p, p - lr * g) for p, g in zip(params,
gradient))) #sgd算法,利用公式4的cost公式搞定8个参数的更新
self.train_function = theano.function([v], monitor,
updates=updates_train)
self.generate_function = theano.function([], v_t, #updates_generate步骤在build_rnnrbm()中产生,音乐的产生主要在那函数中
updates=updates_generate)
def train(self, files, batch_size=100, num_epochs=200):
'''Train the RNN-RBM via stochastic gradient descent (SGD) using MIDI
files converted to piano-rolls.
files : list of strings
List of MIDI files that will be loaded as piano-rolls for training.
batch_size : integer
Training sequences will be split into subsequences of at most this size
before applying the SGD updates.
num_epochs : integer
Number of epochs (pass over the training set) performed. The user can
safely interrupt training with Ctrl+C at any time.'''
assert len(files) > 0, 'Training set is empty!' \
' (did you download the data files?)'
dataset = [midiread(f, self.r,
self.dt).piano_roll.astype(theano.config.floatX)
for f in files] #读取midi文件
try:
for epoch in xrange(num_epochs): #训练200次
numpy.random.shuffle(dataset) #将训练样本打乱
costs = []
for s, sequence in enumerate(dataset): #返回的s是序号,sequence是dataset对应序号下的值
for i in xrange(0, len(sequence), batch_size):
cost = self.train_function(sequence[i:i + batch_size]) #train_function在init()函数中
costs.append(cost)
print 'Epoch %i/%i' % (epoch + 1, num_epochs),
print numpy.mean(costs)
sys.stdout.flush()
except KeyboardInterrupt:
print 'Interrupted by user.'
def generate(self, filename, show=True):
'''Generate a sample sequence, plot the resulting piano-roll and save
it as a MIDI file.
filename : string
A MIDI file will be created at this location.
show : boolean
If True, a piano-roll of the generated sequence will be shown.'''
piano_roll = self.generate_function() #直接生成piano roll文件
midiwrite(filename, piano_roll, self.r, self.dt)#将piano_roll文件转换成midi文件并保存
if show:
extent = (0, self.dt * len(piano_roll)) + self.r
pylab.figure()
pylab.imshow(piano_roll.T, origin='lower', aspect='auto',
interpolation='nearest', cmap=pylab.cm.gray_r,
extent=extent)
pylab.xlabel('time (s)')
pylab.ylabel('MIDI note number')
pylab.title('generated piano-roll')
def test_rnnrbm(batch_size=100, num_epochs=200):
model = RnnRbm()
#os.path.dirname(__file__)为获得当前文件的目录,os.path.split(path)是将path按照最后一个斜线分成父和子的部分
re = os.path.join(os.path.split(os.path.dirname(__file__))[0], #该代码完成的功能是,找到当前文件的上级目录下的/data/Nottinghan/train/*.mid文件
'data', 'Nottingham', 'train', '*.mid') #re得到该目录下的所有.mid文件
model.train(glob.glob(re),#glob.glob()只是将文件路径名等弄成linux的格式
batch_size=batch_size, num_epochs=num_epochs)
return model
if __name__ == '__main__':
model = test_rnnrbm() #该函数主要用来训练RNN-RBM参数
model.generate('sample1.mid') #产生数据的v_t初始化都是0
model.generate('sample2.mid')
pylab.show()
实验总结:
关于bp算法:由于RNN-RBM中对loss函数求导用到了BPTT(back propgation through time)算法:BP算法加入了时间维度。为了加深对BP算法的理解,重新看了一遍推导过程。bp算法的推导过程是主要是由求导中的链式法则得到的。具体算法可参考Martin T.Hagan 的《神经网络设计》第11章(这本书写得不错,翻译得也还可以)。其思想大概为:损失函数F对第m层wij(连接第m层第i个节点和第m-1层第j个节点之间的权值)的导数等于F对第m层第i个节点输入值的导数,乘上该输入值对wij的导数(很容易知道这个导数等于第m-1层第j个节点的输出值)。而F对第m层第i个节点输入值的导数值又等于F对第m+1层输入值的导数(这时需要考虑第m+1中所有的节点)乘以第m+1层输入值对第m层第i个输入值的导数(这个导数值很容易由激发函数的导函数求得),并且我们通常说的bp算法是误差方向传播,这里的第m层误差指的就是F对第m层输入值的导数。由此可知,可以从最后一层依次往前求解,这就是bp算法的思想,本质上是高数里面的链式求导法则。
另外,实验中关于乐理对应的具体细节没有深究。
参考资料:
http://deeplearning.net/tutorial/rnnrbm.html(教程主页)
《神经网络设计》,Martin T.Hagan.
http://www.cse.unsw.edu.au/~waleed/phd/html/node37.html(RNN图片来源1)
Recurrent Neural Networks in Ruby.(RNN图片来源2)
Learning Recurrent Neural Networks with Hessian-Free Optimization, James Martens,Ilya Sutskever.
Modeling Temporal Dependencies in High-Dimensional Sequences: Application to Polyphonic Music Generation and Transcription, Nicolas Boulanger-Lewandowski,Yoshua Bengio,Pascal Vincent.
http://www-etud.iro.umontreal.ca/~boulanni/icml2012(rnn-rbm项目主页)
转自: 作者:tornadomeet 出处:http://www.cnblogs.com/tornadomeet
David 9
Latest posts by David 9 (see all)
- 修订特征已经变得切实可行, “特征矫正工程”是否会成为潮流? - 27 3 月, 2024
- 量子计算系列#2 : 量子机器学习与量子深度学习补充资料,QML,QeML,QaML - 29 2 月, 2024
- “现象意识”#2:用白盒的视角研究意识和大脑,会是什么景象?微意识,主体感,超心智,意识中层理论 - 16 2 月, 2024