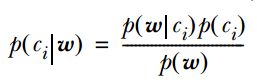这一期, 我们来谈一谈机器学习中的贝叶斯. 概率论中贝叶斯理论, 作为概率的一种“思考方式”, 十分通用. 当机器学习应用中, 贝叶斯的强大理论提现在多个领域, 包括超参数贝叶斯, 贝叶斯推断, 非参贝叶斯等等…
入门
机器学习中的贝叶斯, 首先要区分概率中频率学派和贝叶斯学派的. 网上有各种各样的解释, 其实, 我们可以从机器学习的角度去解释.
机器学习问题可以总结为: 找到一个好的 ![]() 代表一个模型,
代表一个模型, ![]() 表示这个模型的所有参数, 而这个模型就是我们能够训练出的最好模型(至少我们认为是最好的). 什么是最好的模型? 假设有未知数据集
表示这个模型的所有参数, 而这个模型就是我们能够训练出的最好模型(至少我们认为是最好的). 什么是最好的模型? 假设有未知数据集 ![]() , 如果
, 如果 ![]() , 那么这个模型就是最好的. 当然这是不可能的, 也许只有上帝才能对所有的未知100%准确预测. 但我们一定是希望
, 那么这个模型就是最好的. 当然这是不可能的, 也许只有上帝才能对所有的未知100%准确预测. 但我们一定是希望 ![]() 越大越好, 趋向于1.
越大越好, 趋向于1.
如何做到使得 ![]() 越大越好 ? 这就引出了概率论中的两大学派: 传说中的”频率学派”和”贝叶斯学派”. 两大学派区别在哪里? 看下面这个公式:
越大越好 ? 这就引出了概率论中的两大学派: 传说中的”频率学派”和”贝叶斯学派”. 两大学派区别在哪里? 看下面这个公式:
![]()
没错! 这就是大名鼎鼎的贝叶斯公式 ! 机器学习中, ![]() 是真实的训练数据或者抽样数据 .
是真实的训练数据或者抽样数据 . ![]() 是后验概率(posterior)分布 .
是后验概率(posterior)分布 . ![]() 是似然概率(likelihood).
是似然概率(likelihood). ![]() 是先验概率分布(prior).
是先验概率分布(prior). ![]() 是归一化”证据”(evidence)因子.
是归一化”证据”(evidence)因子.
“频率学派”认为, 后验概率和先验概率都是不存在的, 模型 ![]() 不论简单复杂, 参数已经是上帝固定好了的, 只要根据大数定理, 当训练数据足够大, 我们就能找到那个最好的
不论简单复杂, 参数已经是上帝固定好了的, 只要根据大数定理, 当训练数据足够大, 我们就能找到那个最好的 ![]() . 于是公式变为:
. 于是公式变为:
![]()
无论有没有 ![]() , 抽样数据
, 抽样数据![]() 出现的概率都是一样的, 因为任何数据都是从上帝指定的模型中生成的. 于是我们找到
出现的概率都是一样的, 因为任何数据都是从上帝指定的模型中生成的. 于是我们找到 ![]() 的任务就很简单, 最大化
的任务就很简单, 最大化 ![]() 似然概率就行了. 数据量越大, 模型拟合度越高, 我们越相信得到的
似然概率就行了. 数据量越大, 模型拟合度越高, 我们越相信得到的 ![]() 越接近上帝指定的那个
越接近上帝指定的那个 ![]() . 所以”频率学派”预测投硬币正反的概率的方法就是, 投10000次硬币吧, 看看正面出现多少次. 这种基于统计的预测有很多缺点, 首先它指定了一个固定概率, 如果上帝指定的模型不是固定的呢? 另外, 如果数据量不足够大, 预测会不会非常不准确? 当数据维数增大时, 实际计算量也会变得非常大.
. 所以”频率学派”预测投硬币正反的概率的方法就是, 投10000次硬币吧, 看看正面出现多少次. 这种基于统计的预测有很多缺点, 首先它指定了一个固定概率, 如果上帝指定的模型不是固定的呢? 另外, 如果数据量不足够大, 预测会不会非常不准确? 当数据维数增大时, 实际计算量也会变得非常大.
而“贝叶斯学派”认为, 人类的知识是有限的, 我们不知道上帝的安排, 就先假设一个先验(我们已有的知识), 再根据训练数据或抽样数据, 去找到后验分布, 就能知道模型最可能是个什么样子. 继续阅读#2 大话机器学习中的贝叶斯 Bayesian