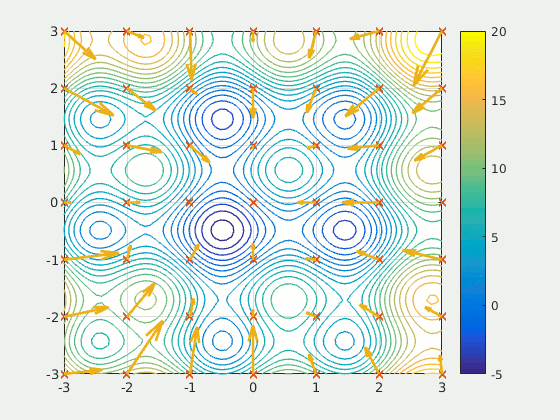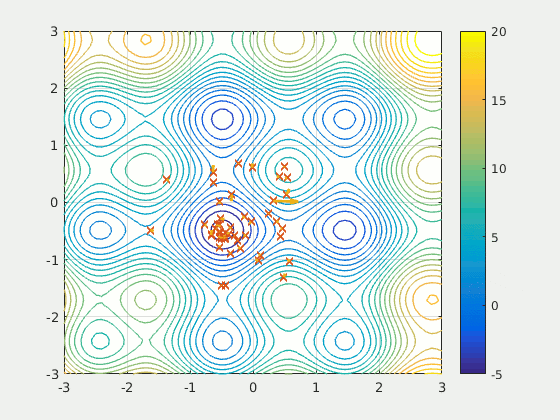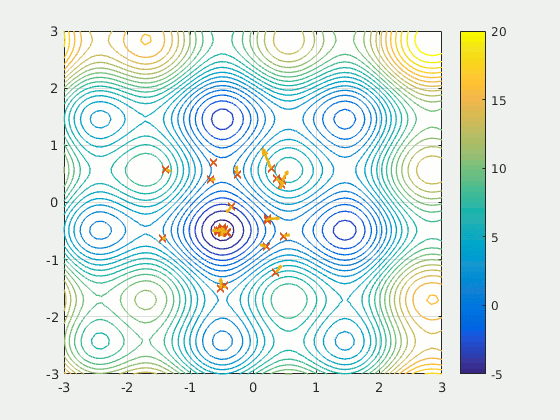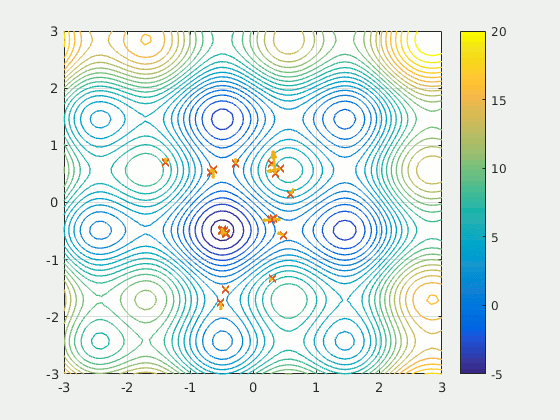AI界的集邮学？回眸ES，粒子群PSO，遗传(进化)算法，GA等无梯度优化方法

“盾从防御看是美的，矛则从射击的敏捷和力量看是美的”

—— 苏格拉底

实验物理学家卢瑟福说过：“所有科学要么是物理，要么是集邮” 。相较其他学科，物理学也许对宇宙大一统的解释有一定的优越性。如在研究半衰期过程中就会被一种大自然的神奇所折服（弱核力）。

然而“集邮”并不是没有意义。苏格拉底说过，“盾从防御看是美的，矛则从射击的敏捷和力量看是美的”。不能因为深度学习理论薄弱，就去否认深度网络的实际效用。收集大自然的“邮票”加以利用也许成就感不那么高，但它可能非常有效 ，甚至在某些角度不乏美感。

比如在我们AI机器学习领域就有这样一种“集邮”学：其囊括遗传算法，进化策略算法（ES），粒子群算法（PSO），多数都是以模仿自然为依据，还有一个流行好听的称呼：无梯度优化算法（gradient-free，derivative-free）（facebook开源的Nevergrad库也是来自这种优化方法）

这些“离经叛道”的优化算法，不像SVM极具数学根基，但在某些场合非常适用：

拿粒子群算法（PSO）来讲，如上图，是粒子群在平面上找到极小值的过程，其本质是模拟了群鸟飞行或群鱼相互协作的搜索过程：

其核心公式也是贯彻了相互协作的原则：

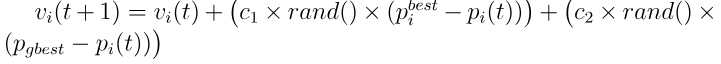
其中vi(t+1)是下一个时刻的粒子速度，它由三个因素决定：

1. vi(t)即当前速度，

2. 该粒子历史最佳位置与该粒子当前位置pi(t)的差,

3. 群体历史最佳位置与该粒子当前位置pi(t)的差 。值得注意的是，这里说的速度和差都是矢量。

用人话来说就是每个粒子的方向是由群体最佳方向和自己搜索的最佳方向共同决定的。

是的，也许这种算法看不出坚实的理论基础，但是在所有的搜索算法中，David 9认为这何尝不是一类最有美感的算法？加之如果融合之前提到的量子计算优势，不排除无梯度优化算法今后还会有长足的进步。

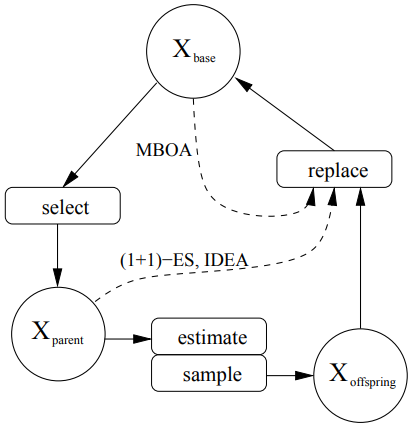
回望无梯度优化，进化策略（ES）是不可忽视的一大类。

而ES算法框架大体都是一样的：

如上图，圆圈是群体集合，矩形框是操作，实线是所有ES算法都有的过程，虚线是一些特别ES算法需要的过程。即，一般算法流程为：

1. 从Xbase基础群体集合中选择出Xparent父代群体集合
2. 从 Xparent 父代群体集合估算出目前的整体概率分布
3. 从2中的分布抽样出Xoffspring子代群体集合
4. 用Xoffspring 子代群体集合替代 Xbase 基础群体集合

之所以有虚线，是因为替代基础集合的过程也可以由父代群体参与（(1+1)-ES算法和IDEA算法），因父代也有较好的个体不需要淘汰。

论文[8]很好地比较了5个ES算法（ (1+1)-ES，CSA-ES，CMA-ES，IDEA，MBOA ）之间的微妙区别:

1.对于概率分布和分布参数：

所有ES算法都是借助高斯模型N(m, C)做底层搜索的。不一样的是 (1+1)-ES和CSA-ES算法用的是各方向等距的高斯（C= ），而CMA-ES和IDEA算法用的是更随意方向的高斯（如CMA-ES用协方差矩阵来控制步长）

另外IDEA算法和MBOA算法的分布参数在每次迭代时都会改变， 如IDEA在每次迭代时都构造新的条件分解图。 MBOA算法也会不断更新自己的高斯核。

2. 在训练过程中使用的统计度量：

ES算法的分布都是被群体个体的位置和每个个体各自的表现（适应度）左右的。不同的是 (1+1)-ES只关注了父代到子代的遗传率；而 CSA-ES 和CMA-ES都维护了整个种群的进化路线，从而引导下一次子代父代更替；IDEA在构图时还考虑了父代的度量。

3. 学习策略和历史信息的使用：

更新有两种完全不同的策略：一种是完全根据进化来出的子代群体的分布更新概率分布；另一种是每次都根据群体的情况重新构造全新的概率分布（就好像每次都是诺亚方舟创世）。

对于历史信息的保留方式也有两种：

一种是每一代都保留优秀的子代，用于后续的迭代，

另一种是一直维护自身的内部参数来更新每一次的代际更替。

参考文献：

1. https://github.com/facebookresearch/nevergrad
2. https://github.com/DEAP/deap
3. http://www.jmlr.org/papers/volume13/fortin12a/fortin12a.pdf
4. http://vision.gel.ulaval.ca/~cgagne/pubs/sigevolution2014.pdf
5. https://cloud.tencent.com/developer/article/1379395
6. https://zh.wikipedia.org/wiki/欧内斯特·卢瑟福
7. https://en.wikipedia.org/wiki/Particle_swarm_optimization
8. Learning Probability Distributions in ContinuousEvolutionary Algorithms – A Comparative Review
9. http://www.cleveralgorithms.com/nature-inspired/swarm/pso.html

本文采用署名 – 非商业性使用 – 禁止演绎 3.0 中国大陆许可协议进行许可。著作权属于“David 9的博客”原创，如需转载，请联系微信: david9ml，或邮箱：yanchao727@gmail.com

或直接扫二维码: