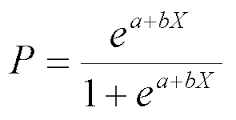今天拜读南大周志华老师今年1月的新书《机器学习》, 决定趴一趴Logistic Regression. 在各种书籍, 网络中它们翻译各不相同, 有叫”逻辑回归”的, 也有叫”对数回归” “的, 也有叫”对数几率回归”. 其实, 这几个概念都是同一个概念.
当然, 我是认为周志华老师的”对数几率回归”的说法比较恰当.
那David 9我就来当个”传教士”, 说说什么是”对数几率回归”, 为什么要叫”对数几率回归” ?
说”对数几率回归”, 我们必须从”线性回归”和”广义线性回归”说起:
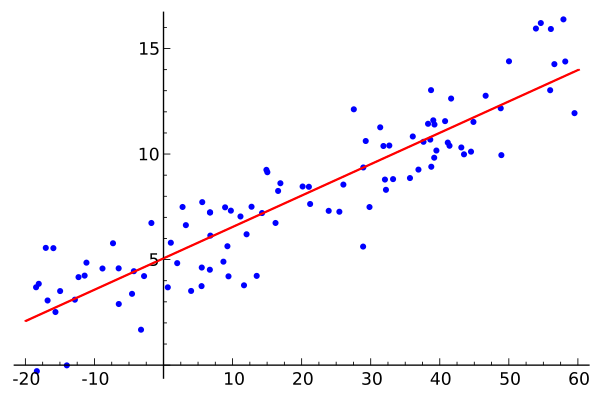
线性回归非常简单, 给你一个样本集合![]() , 注意这里
, 注意这里![]() 可以都是高维向量
可以都是高维向量
于是目标是找到一个好的线性模拟:
![]()
求出w, b, 这个模型就算固定了. 如何衡量样本y和你的f(x)之间的差别, 每个人都有不同的方法, 最常用的, 当然是最小二乘法, 也就是用欧氏距离去衡量.
Whatever ~ 我们用一条线去模拟和预测未来的数据, 即, 给我一个x值, 我能给你一个预测的y值, 这就是线性回归.
“广义线性回归”又是怎么回事?
也非常简单, 我们不再只是用线性函数模拟数据, 而是在外层加了一个单调可微函数g, 即:
![]()
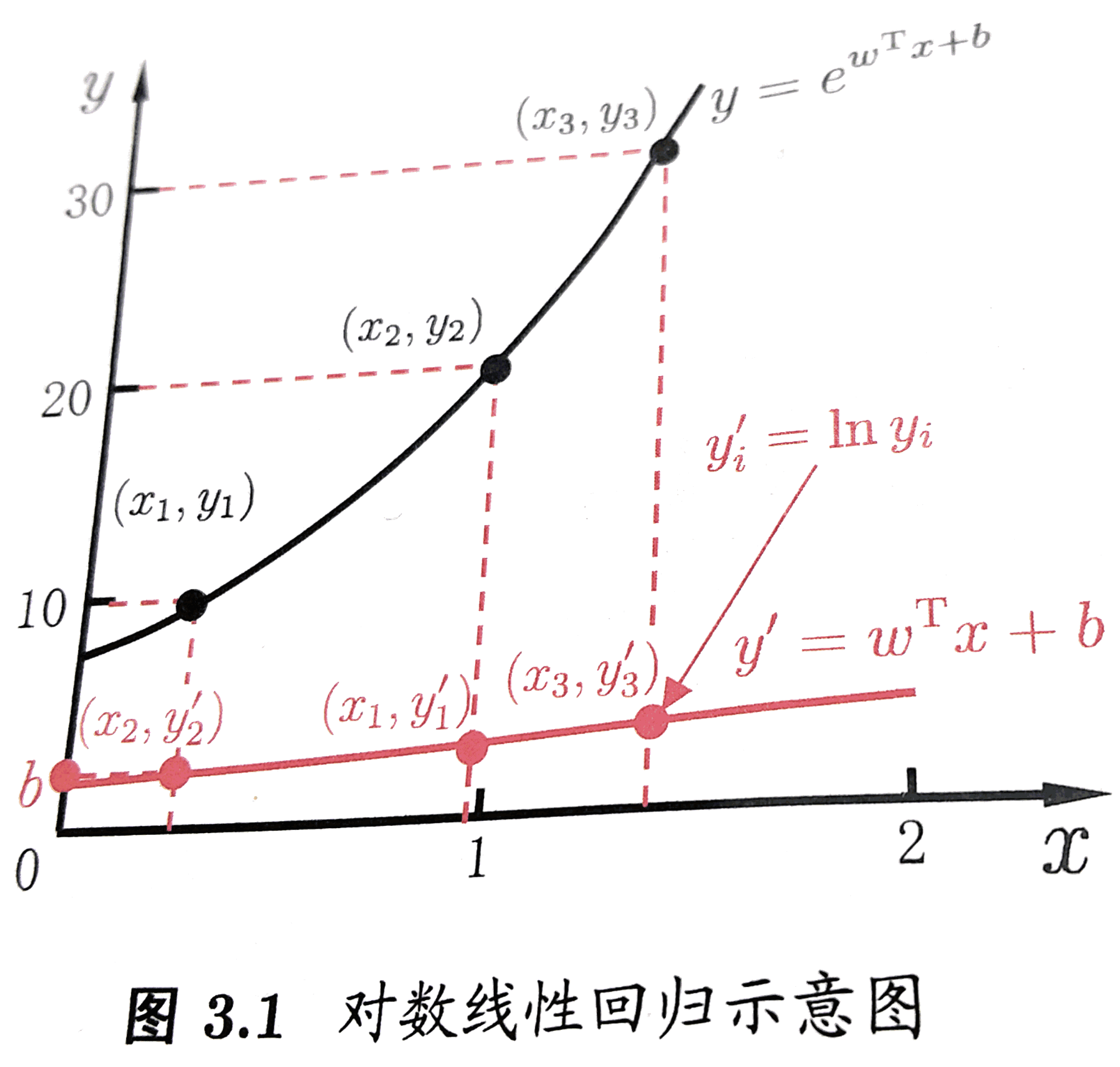
如果g=ln , 则这个广义线性模型就变为对数线性回归. 其实本质就是给原来线性变换加上一个非线性变换(或者说映射), 使得模拟的函数有非线性的属性, 但是, 本质上调参还是线性的, 主体是内部线性的调参. 来一发《机器学习》中的直观截图:
是的, 如果我们觉得模型应该是指数变化的时候, 我们可以简单粗暴地把线性模型映射到指数变化上, 如图中的红线映射到黑色的指数线. 这就是广义线性模型的思想.
但问题来了, “对数几率回归”是咋回事? 和”对数线性回归”有什么关系?
事实上, “对数几率回归”不是解决回归问题的, 而是解决分类问题的. 目的是要构造一个分类器Classifier. 并且, 关键不在于”回归”, 不在于如何用最大似然训练函数, 也不在于用什么最优化方法训练函数. 关键在于”对数几率”这四个字, 在于对数几率函数.
为了解决一个最简单的二类分类问题, 我们为每一个点定义一个值域[0, 1]的函数, 表示这个点分在A类或者B类中的可能性, 如果非常可能是A类, 那可能性就逼近1, 如果非常可能是B类, 那可能性就逼近0(相对A的可能性), 如果两个类很难判别, 当然就是0.5. 于是构造出对数几率函数:
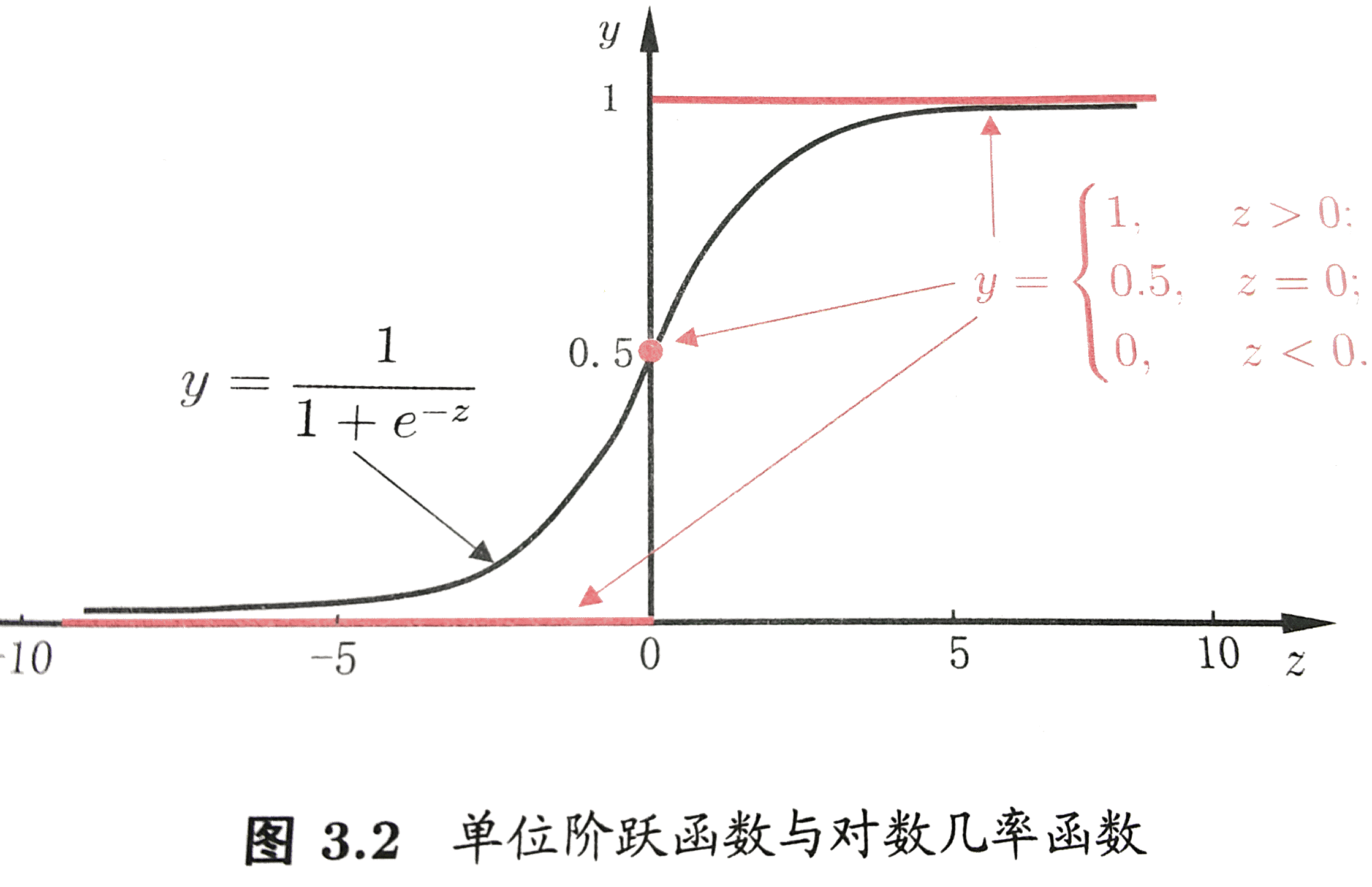
是不是很熟悉? 自然对数在分母上. 没错它是一种”Sigmoid”函数.
这里的z就是![]()
于是, 一个点归在A类的可能性的终极形态就是:
是不是? 和”回归”没啥关系吧? 它关注的是一个点分在A类的可能性.
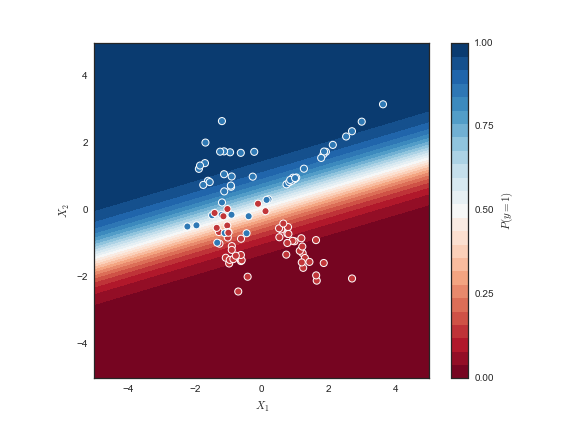
来瞧瞧最后训练出的模型:
蓝颜色越深, 模型认为y=1的可能性越大, 反之, 红颜色越深, 模型认为y=1的可能性越小.
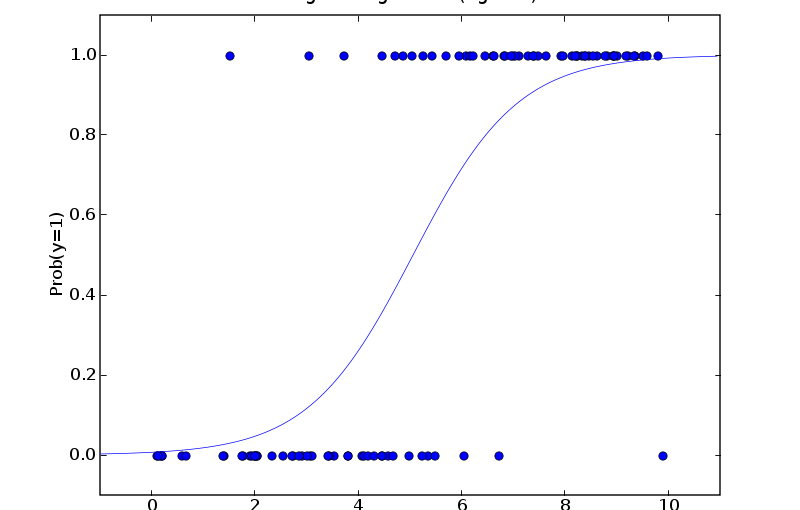
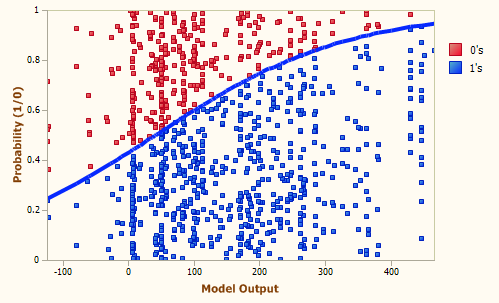
再来看看这张:
注意y轴是可能性, 说明x轴越大, 蓝色样本的可能性越大.
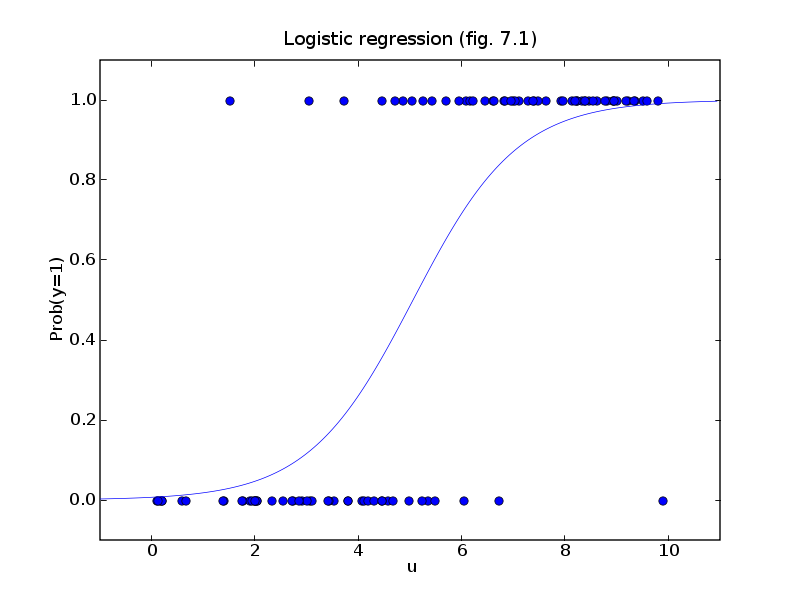
下面这张图也一样:
y=1的可能性随着u值的增加而增加.
因此, “对数几率回归”(Logistic Regression)做的事情是对分类的可能性建模, 而不是去预测样本的y值 !
参考文献:
- https://en.wikipedia.org/wiki/Linear_regression
- https://en.wikipedia.org/wiki/Generalized_linear_model
- http://stackoverflow.com/questions/28256058/plotting-decision-boundary-of-logistic-regression
David 9
Latest posts by David 9 (see all)
- 修订特征已经变得切实可行, “特征矫正工程”是否会成为潮流? - 27 3 月, 2024
- 量子计算系列#2 : 量子机器学习与量子深度学习补充资料,QML,QeML,QaML - 29 2 月, 2024
- “现象意识”#2:用白盒的视角研究意识和大脑,会是什么景象?微意识,主体感,超心智,意识中层理论 - 16 2 月, 2024