有时一件事做的不够好，不是准备的不够好，只是因为我们不够“聪明”。 —— David 9
神经网络一个有意思的地方是，它的信息容量总是比要处理的问题大，它的复杂度往往是“过剩”的。但是其他传统模型，包括今天聊的贝叶斯概率模型世界，复杂度就不能简单地用“加深层数”和“跳层连接”实现，这些模型，增加模型复杂度就要用其他“聪明”些的方式。
在贝叶斯模型世界（如VAE，pPCA），所担心的不是神经网络的“梯度消失”或“梯度爆炸”，而是“后验失效”(posterior collapse)现象。本质上，任何模型（传统或非传统）都要从每个新样本“汲取信息”，更新自身。当信息无法汲取并用来更新模型，就会出现上述问题。
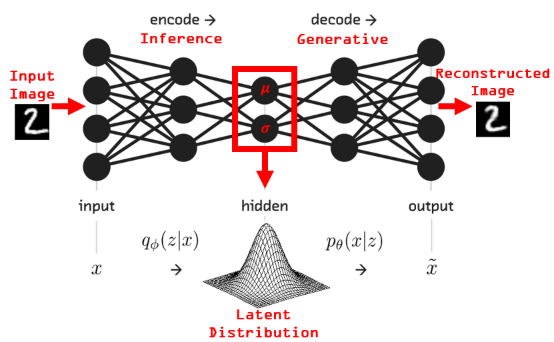
不同的是，GAN(或神经网络)信息传递是内部“混沌”的，VAE的信息传递在内部总要映射到一个假想的隐变量z的分布上（常见高斯分布）：
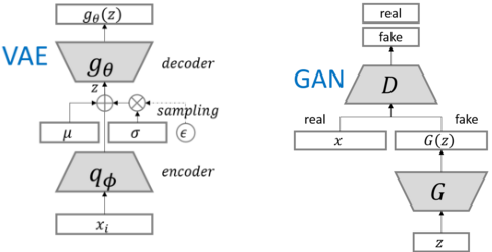
即，GAN训练的是如何生成一个样本，而VAE训练的是如何生成一个分布（这个分布可以生成样本）。
VAE的变分推断中，直接计算数据x的相似度边际分布log p(x) 非常困难，但是可以用变分分布q(z|x)去估计后验（实际上变分分布就是VAE的编码器encoder），这就引出了VAE的目标函数，ELBO，即the Evidence Lower Bound：
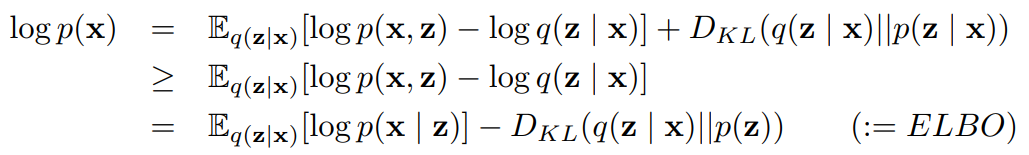log p(x)一定是大于ELBO的，那么让ELBO最大就是VAE的最终解了：
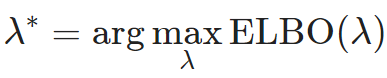ELBO的广泛使用使得“后验失效”(posterior collapse)现象的根源看似就是ELBO目标函数。 继续阅读重新认识ELBO，对“后验失效”(posterior collapse)问题的新理解，探索VAE，pPCA和贝叶斯模型世界