EM是我一直想深入学习的算法之一，第一次听说是在NLP课中的HMM那一节，为了解决HMM的参数估计问题，使用了EM算法。在之后的MT中的词对齐中也用到了。在Mitchell的书中也提到EM可以用于贝叶斯网络中。
下面主要介绍EM的整个推导过程。
1. Jensen不等式
回顾优化理论中的一些概念。设
是定义域为实数的函数，如果对于所有的实数
，
，那么是凸函数。当x是向量时，如果其hessian矩阵H是半正定的（
），那么是凸函数。如果
或者
, 那么称是严格凸函数。
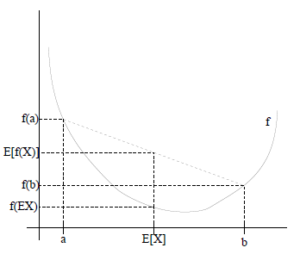
Jensen不等式表述如下：
如果f是凸函数，X是随机变量，那么
特别地，如果是严格凸函数，那么
当且仅当，也就是说
是常量。
如果用图表示会很清晰：
