今天David 9要带大家读偶像Hinton等大牛的一篇论文，搞深度学习或者DL的朋友应该知道，那就是有名的Dropout方法。
学过神经网络的童鞋应该知道神经网络很容易过拟合。而且，如果要用集成学习的思想去训练非常多个神经网络，集成起来抵制过拟合，这样开销非常大并且也不一定有效。于是，这群大神提出了Dropout方法：在神经网络训练时，随机把一些神经单元去除，“瘦身”后的神经网络继续训练，最后的模型，是保留所有神经单元，但是神经的连接权重
乘上了一个刚才随机去除指数
.
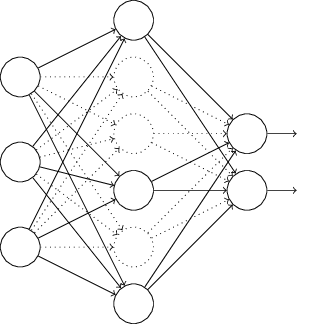
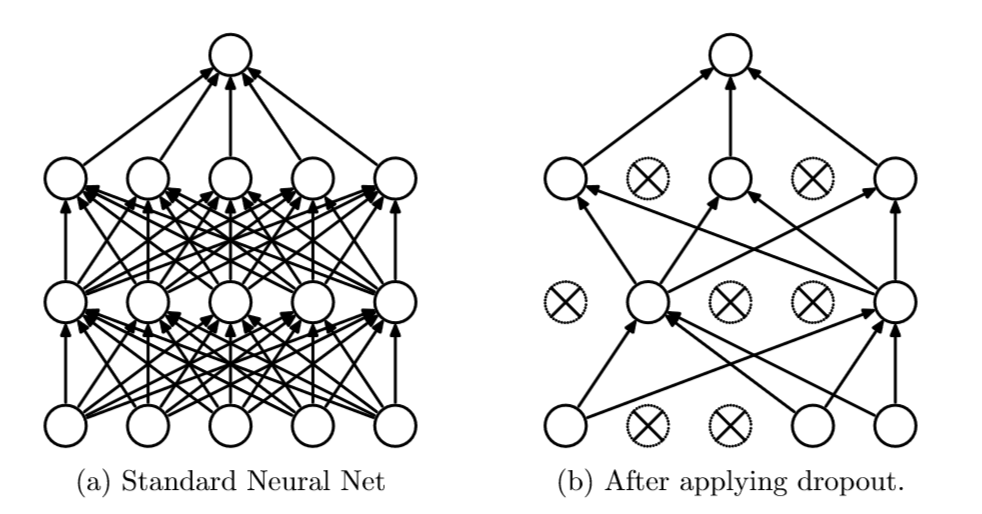
废话少说，上原理图：
左边是标准神经网络，右边是使用Dropout的神经网络，可见只是连接度少了一些，并不影响模型继续训练。其实，Dropout动机和初衷非常有意思。 继续阅读神经网络抵制过拟合神器：Dropout 手把手论文入门 — 深度学习 DL 番外篇
总结： 我总是从迷你程序中学到很多。这个教程用python写了一个很简单迷你程序讲解递归神经网络。
递归神经网络即RNN和一般神经网络有什么不同？出门左转我们一篇博客已经讲过了传统的神经网络不能够基于前面的已分类场景来推断接下来的场景分类，但是RNN确有一定记忆功能。废话少说，上图：
EM是我一直想深入学习的算法之一，第一次听说是在NLP课中的HMM那一节，为了解决HMM的参数估计问题，使用了EM算法。在之后的MT中的词对齐中也用到了。在Mitchell的书中也提到EM可以用于贝叶斯网络中。
下面主要介绍EM的整个推导过程。
回顾优化理论中的一些概念。设
是定义域为实数的函数，如果对于所有的实数
，
，那么是凸函数。当x是向量时，如果其hessian矩阵H是半正定的（
），那么是凸函数。如果
或者
, 那么称是严格凸函数。
Jensen不等式表述如下：
如果f是凸函数，X是随机变量，那么
特别地，如果是严格凸函数，那么
当且仅当，也就是说
是常量。
如果用图表示会很清晰：
