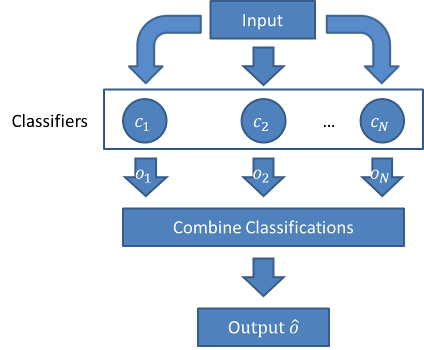
聊聊集成学习和"多样性", "差异性"的那些事儿~ | David 9的博客 --- 不怕"过拟合"

在第3期 “#3 集成学习–机器学习中的群策群力” 中我们谈到, 集成学习是使用一系列学习器进行学习，以某种规则把各个学习结果进行整合，从而获得比基学习器有更好学习效果的集成学习器.

集成学习之所以有更好的学习效果, 与单个基学习器的“多样性”或者说“差异性”密不可分.

正像大自然万物的多样性随处可见, 生物繁衍产生下一代的过程.

集成学习的关键是允许每个单个学习器有各自的差异性, 同时又有一定错误率上界的情况下, 集成所有单个学习器. 正如在繁衍下一代时, 父母各自贡献自己的DNA片段, 取长补短, 去重组得到新的下一代基因组合.

对此, [Krogh and Vedelsby, 1995]给出了一个称之为”误差-分歧分解“(error-ambiguity decomposition)的漂亮式子:

$E =\overline{E} - \overline{A}$

$E$ 表示集成后模型的泛化误差.

$\overline{E} = \sum_{i=1}^{T} w_iE_i$ 表示个体学习器范化误差的加权均值.

$\overline{A} = \sum_{i=1}^{T} w_iA_i$ 表示个体学习器的加权分歧项, 即个体学习器差异性的度量最后加权平均.

这个式子表明: 个体学习器准确性越高, 同时, 多样性越大, 则集成效果越好.

但是同时做到这两点, 其实在实际训练中是有难度的. 因为不能直接去优化 $\overline{E} - \overline{A}$ , 难以直接用 $\overline{E} - \overline{A}$ 作为优化对象.

好了, 根据核心式子 $E =\overline{E} - \overline{A}$ , 我们知道, 集成学习模型的优劣与所有单个学习器的”多样性”, 或”差异性”息息相关.

那么, 如何增强集成学习时的多样性 ? 书上提供了几种多样性增强方法:

数据样本扰动

数据样本扰动通常是基于采样法, 给定初始数据集, 可从中产生不同数据子集, 再利用不同数据子集训练出不同的个体学习器(或称基学习器). 常见的基学习器, 例如决策树, 神经网络等, 训练样本稍加变化就会导致学习器有显著变动, 数据样本扰动法对这样的”不稳定学习器“很有效.

但是, 有一些基学习器, 对数据样本扰动不敏感, 例如线性学习器, 支持向量机, 朴素贝叶斯, k邻近学习器等, 这样的学习器称为”稳定学习器“.

输入属性扰动

训练样本通常由一组属性描述, 不同的”子空间”(subspace), 提供了观察数据的不同视角. 随机子空间(random subspace)算法[Ho, 1998]就依赖于输入属性扰动, 从初始属性集中抽取若干个属性子集, 再基于每个属性子集训练一个基学习器, 算法描述如下:

输出表示扰动

有时候我们也可以用如”翻转法”(Flipping Output)[Breiman, 2000]随机改变一些训练样本的标记. 也可以用如”输出调整法”(Output Smearing)[Breiman, 2000]将分类输出转化为回归输出后构建个体学习器. 总之, 是一些对输出的变换操控.

算法参数扰动

对基学习器的参数, 进行不同的配置, 也可以达到训练出多样基学习器的目的. 例如, 神经网络的隐层神经元个数, 初始连接权值等, 通过随机设置不同参数, 往往可以产生差别较大的个体学习器.

另外, 不同的多样性增强方法, 可以同时使用.

参考文献:

邮箱：yanchao727@gmail.com 微信: david9ml

聊聊集成学习和”多样性”, “差异性”的那些事儿~