用python做贝叶斯A/B测试 — 贝叶斯A/B测试入门以及“共轭先验”是什么？

如果不再假设一个分布的参数是固定的，而是去寻找这个参数可能的分布，就可以理解超参数的意义 — David 9

A/B测试一直是David 9想cover的知识点，今天又邂逅一篇相关文章：“tl;dr Bayesian A/B Testing with Python”。于是今天决定讲解一下如何“用python做贝叶斯A/B测试”。所以，现在，两个重要的知识点是 A/B 测试 和 “共轭先验”。

关于A/B测试，其实概念非常简单，简单来说，就是为同一个目标制定两个方案（比如两个页面），让一部分用户使用 A 方案，另一部分用户使用 B 方案，记录下用户的使用情况，看哪个方案更符合设计。A/B测试已经在Web上得到广泛的应用，可以用于增加转化率注册率等网页指标[3].

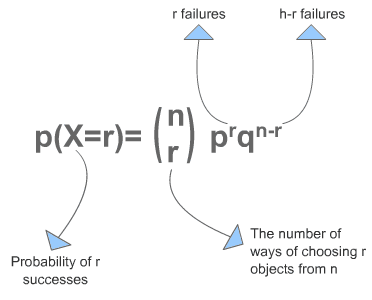
很显然，A方案的转化率可以看作一个二项分布：

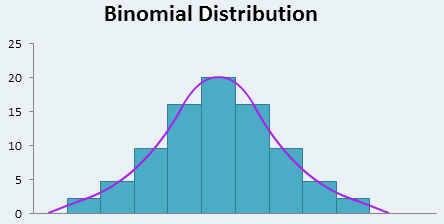
A方案的转化率分布就需要一个分布参数p，表示转化率的可能性。传统的频率学派会把实验总数中所有转化率的总数除以实验总数，得到这个p。以这个p为峰值获得一个类似高斯分布，大概像这样：

然而，贝叶斯学派不会假设p是固定不变的，他们会引入一个Beta分布作为二项分布的共轭先验，通过调整Beta分布参数，动态调整p的值.

Beta分布是什么？

Beta分布是二项分布的共轭先验。用大白话讲是，Beta分布描述了二项分布中p取值的可能性，这一分布相当合理：

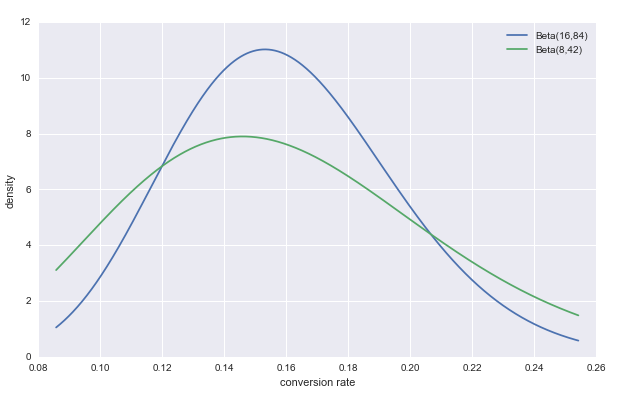
上图是一枚硬币抛100次有16次正面，和抛50次有8次正面的两个实验各自的Beta分布。可以注意到，Beta分布有两个参数α和β，α的现实意义就是16次正面，β的现实意义就是84次反面。

所以通俗地讲，Beta概率是对“正面概率应该为p”这件事情的概率分布。

有意思的是，上图抛100次有16次正面和抛50次有8次正面虽然只是实验规模不同，但是分布密度图是不一样的：

第一：频率学派观点是应该猜测正面概率p=0.16；贝叶斯学派观点是，以上两种情况的猜测p都小于0.16，因为实验次数越少，真实的正面和反面的差距就可能越大！

第二：实验次数越小，上面概率密度图应该越平缓（绿线），因为少的实验次数不能增大决策信心。而蓝色的100次实验，明显有更大的信心猜测p更接近0.16.

第三：实验次数越大，上面概率密度图的均值更应该接近0.16，符合大数定律。

是不是相当合理！

很自然地，可以把Beta分布运用到我们日常的A/B测试。

但是写代码前，让我们先了解一个更有意义的话题：

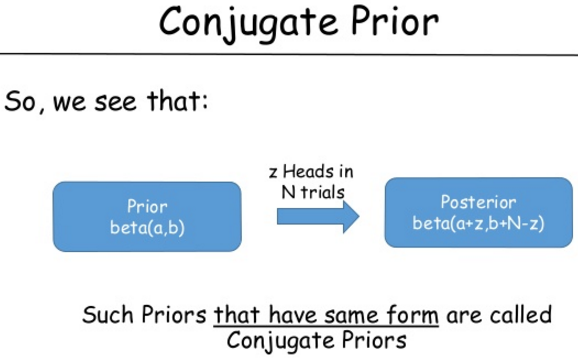
什么是共轭先验？

关于共轭先验需要记得两个关键点：

共轭关系是指似然概率和先验概率共轭！就是说，对于一个特定的似然函数，我们可以找到一个先验概率，叫做这个似然函数的共轭先验。
那符合什么条件才能叫共轭先验？找到这个先验概率后，如果符合：似然函数乘以先验概率后，得到的后验概率也是和先验概率一样的形式，那么就可以了！

如上图，先验概率是参数为的Beta分布，似然概率（Likelihood）是伯努利分布，那么后验概率计算后也是Beta分布，只是参数为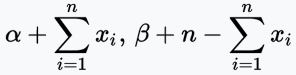

这里只是参数不同了而已，先验和后验都是Beta分布！这时我们就把Beta分布叫做伯努利分布的共轭先验！这里Beta分布的两个参数又叫超参数，因为Beta分布好似是伯努利分布的分布，可以通过不断迭代更新超参数，生成更好的伯努利分布或二项分布。

超参数相当容易迭代，因为先验和后验是一个形式。这一次的迭代结果可以作为下一次迭代的开始。

好了~ 最后让我们跑一些有趣的代码，来巩固A/B测试，Beta分布，以及“共轭先验”的相关知识。

模拟两个Beta分布，假设抛50次有8次正面（也可以理解为50个人的网页转化率）：

from scipy.stats import beta
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import seaborn as sns

people_in_branch = 50

# Control is Alpaca, Experiment is Bear
control, experiment = np.random.rand(2, people_in_branch)

c_successes = sum(control < 0.16)

# Bears are about 10% better relative to Alpacas
e_successes = sum(experiment < 0.176)

c_failures = people_in_branch - c_successes
e_failures = people_in_branch - e_successes

# Our Priors
prior_successes = 8
prior_failures = 42



# For our graph
fig, ax = plt.subplots(1, 1)

# Control
c_alpha, c_beta = c_successes + prior_successes, c_failures + prior_failures
# Experiment
e_alpha, e_beta = e_successes + prior_successes, e_failures + prior_failures

x = np.linspace(0., 0.5, 1000)

# Generate and plot the distributions!
c_distribution = beta(c_alpha, c_beta)
e_distribution = beta(e_alpha, e_beta)

ax.plot(x, c_distribution.pdf(x))
ax.plot(x, e_distribution.pdf(x))

ax.set(xlabel='conversion rate', ylabel='density')
fig.show()
import pdb; pdb.set_trace()  # XXX BREAKPOINT

实验次数太少，我们改进一下：

more_people_in_branch = 4000

# Control is Alpaca, Experiment is Bear
control, experiment = np.random.rand(2, more_people_in_branch)

# Add to existing data
c_successes += sum(control < 0.16)
e_successes += sum(experiment < 0.176)

c_failures += more_people_in_branch - sum(control < 0.16)
e_failures += more_people_in_branch - sum(experiment < 0.176)

再画个PPF试试：

# Arguments are x values so use ppf - the inverse of cdf
print(c_distribution.ppf([0.025, 0.5, 0.975]))
print(e_distribution.ppf([0.025, 0.5, 0.975]))

# [ 0.14443947  0.15530981  0.16661068]
# [ 0.15770843  0.16897057  0.18064618]

计算p-values指标：

sample_size = 100000

c_samples = pd.Series([c_distribution.rvs() for _ in range(sample_size)])
e_samples = pd.Series([e_distribution.rvs() for _ in range(sample_size)])

p_ish_value = 1.0 - sum(e_samples > c_samples)/sample_size

# 0.046830000000000038

p-values指标小于0.05，我们有信心相信银币反面概率更可能较大。

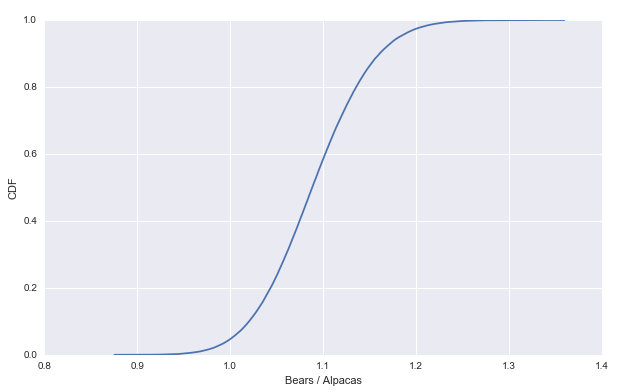
最后画个CDF图试试：

fig, ax = plt.subplots(1, 1)

ser = pd.Series(e_samples/c_samples)

# Make the CDF
ser = ser.sort_values()
ser[len(ser)] = ser.iloc[-1] 
cum_dist = np.linspace(0., 1., len(ser))
ser_cdf = pd.Series(cum_dist, index=ser)

ax.plot(ser_cdf)
ax.set(xlabel='Bears / Alpacas', ylabel='CDF')