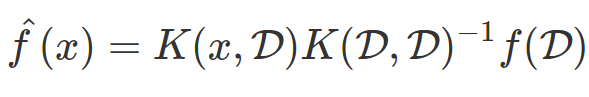“数据驱动”的模型被数据限制，关键在于，它被如何限制？ —— David 9
在上一期“具身智能”的诱惑中我们就提到，智能体不会是孤立的，他处于特定的环境中，他与环境交互并适应环境，塑造环境并与之交融。
同样，在一个数学系统中，有及其相似之处。伯克利最新的研究揭示了（或部分揭示了）神经网络泛化能力的第一性原理（A First-Principles Theory）。
其研究大量依赖于NTK神经正切核的实验，曾经David也在星球中聊过正切核和无限宽网络，其本质上都是构建一个“核系统”，并找出一个“核回归”方法，
能够很好地近似真实分布 f：
其中学习到的近似分布即：
而K代表的核函数即系统中衡量元素直接距离的函数。
伯克利的研究人员指出这种学习系统就是典型的核回归方法，而核回归和NTK已经神经网络的关系如下:
进一步地，对于无限宽网络和核回归方法，其对称性和半正定的性质，使得我们总可以找到一组正交的特征向量，使得每一对特征值和特征向量
都满足：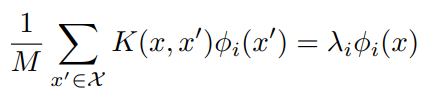
这就引出一个洞见：既然一个特征向量代表一个学习函数，其对应的特征值代表这个函数的特征，那么，某一个特征函数对某一个样本的判断，
