我们经常在各类算法中看到”蒙特卡罗”(Monte Carlo)的字样, 比如MCMC(Markov Chain Monte Carlo) , 还有AlphaGo使用的蒙特卡洛搜索树. 其实, “蒙特卡罗”并不是一个特定算法, 它是一个思想或者方法的统称. 听起来很神秘, 其实用正常”人话”就能简单解释.
维基百科对蒙特卡罗方法(英语:Monte Carlo method)给出的解释是:
二十世纪四十年代中期由于科学技术的发展和电子计算机的发明,而被提出的一种以概率统计理论为指导的一类非常重要的数值计算方法。是指使用随机数(或更常见的伪随机数)来解决很多计算问题的方法。
与它对应的是确定性算法。
所以说, 蒙特卡罗算出的值, 不是精确的而是一个估计, 但是在人们可以接受的错误范围.
下面是维基百科上一个很直观的例子:
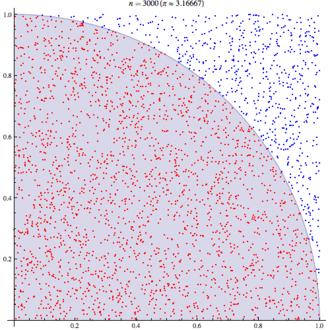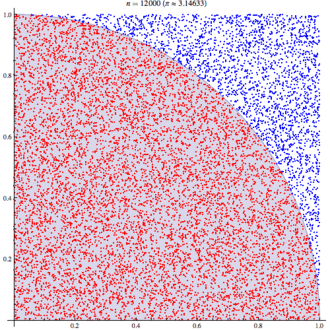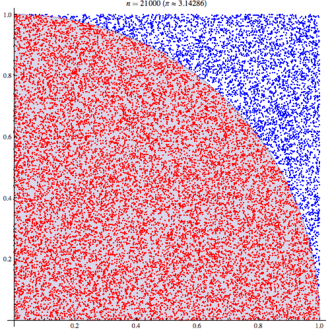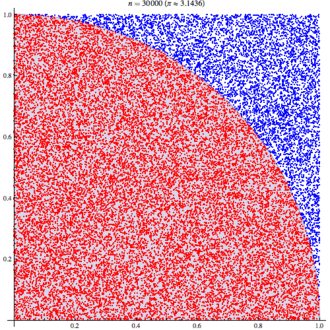
使用蒙特卡洛方法估算π值. 放置30000个随机点后,π的估算值与真实值相差0.07%.
这张图其实很简单, 就像我们玩飞镖一样, 随机地在一个方形平面上投掷30000个飞镖, 事先我们并不知道圆周率π的值究竟是多少, 但是我们知道这里有1/4的圆, 于是我们把红色面积上的点数m, 和蓝色面积上的点数n, 以及圆周率π的关系, 可以写出一个约等于的式子:
π ≈ 4m/(n+m)
随着m+n的投射点的逐渐增加, π值的计算也越来越精确, 最后我们就估计出一个不错的比较精确的π值啦
大家看这个是不是在哪里很熟悉? 没错, 就是大数定律的思想嘛… 只不过大数定理强调统计学中的极限和期望, Monte Carlo方法这是计算机中的模拟, 用有限随机数去计算估计值.
所以Monte Carlo只是这种思想的统称, 与特定算法结合会有不同表现形式.
当然Monte Carlo不只是能估计值那么简单, 它可以用来估计未知分布, 未知模型参数, 等等, 所以在很多抽样方法中有Monte Carlo的身影, 比如大名鼎鼎的MCMC.
接下来我们来趴一趴蒙特卡罗方法的历史:
20世纪40年代,在冯·诺伊曼,斯塔尼斯拉夫·乌拉姆和尼古拉斯·梅特罗波利斯在洛斯阿拉莫斯国家实验室为核武器计划工作时,发明了蒙特卡洛方法。因为乌拉姆的叔叔经常在蒙特卡洛赌场输钱得名,而蒙特卡罗方法正是以概率为基础的方法。
蒙特卡罗方法的名字来源于摩纳哥的一个城市蒙地卡罗,该城市以赌博业闻名,大家都知道, 赌钱这个问题, 一般是没有精确解的. 但是, 只要你是个老赌徒, 那最后, 你会对整个赌局有更全面的认识, 不是吗?
参考文献:
https://zh.wikipedia.org/wiki/%E8%92%99%E5%9C%B0%E5%8D%A1%E7%BE%85%E6%96%B9%E6%B3%95
David 9
Latest posts by David 9 (see all)
- 修订特征已经变得切实可行, “特征矫正工程”是否会成为潮流? - 27 3 月, 2024
- 量子计算系列#2 : 量子机器学习与量子深度学习补充资料,QML,QeML,QaML - 29 2 月, 2024
- “现象意识”#2:用白盒的视角研究意识和大脑,会是什么景象?微意识,主体感,超心智,意识中层理论 - 16 2 月, 2024


你好,请问小编可以让我转载这篇文章内容吗?我会备注原文出处链接的以及作者
[url=http://rsc.hbust.com.cn]ca88[/url]
可以 请备注原文出处链接的以及作者