David 9的博客 — 不怕"过拟合"

世界有时丑陋，我们需要遗忘。

但“遗忘”往往不是我们想的那样。 — David 9

我们很容易注意到，“记忆”或“遗忘”是一件很复杂的事情，对一般人，那些痛苦失落的时光往往印象深刻，但曾经那些快感或幸福会转瞬即逝快速模糊。并且，“主动遗忘”和“彻底遗忘”经常是不存在的事情，更不用说长时记忆与短时记忆究竟是什么？

事实上，记忆是从哪里来的我们都不完全了解，科学家曾经在软体动物身上做实验，把一部分A个体的RNA移植到B, 从而B拥有了A的行为记忆，

试想对于人体，基因对记忆本身的影响更复杂难料。

回归主题，退一步，如果仅仅考虑“彻底遗忘”，并且是在模型层面的遗忘，或许问题会简单一点。

而且把遗忘聚焦在简单的“数据遗忘”，多伦多大学向量学院SISA方法提供了很好的参照。即，把某个训练数据从对神经网络影响中剔除。SISA方法展开是：Sharding(分片)，Isolation(隔离)， Slicing(切割)，Aggregation(聚合)，大致架构如下：

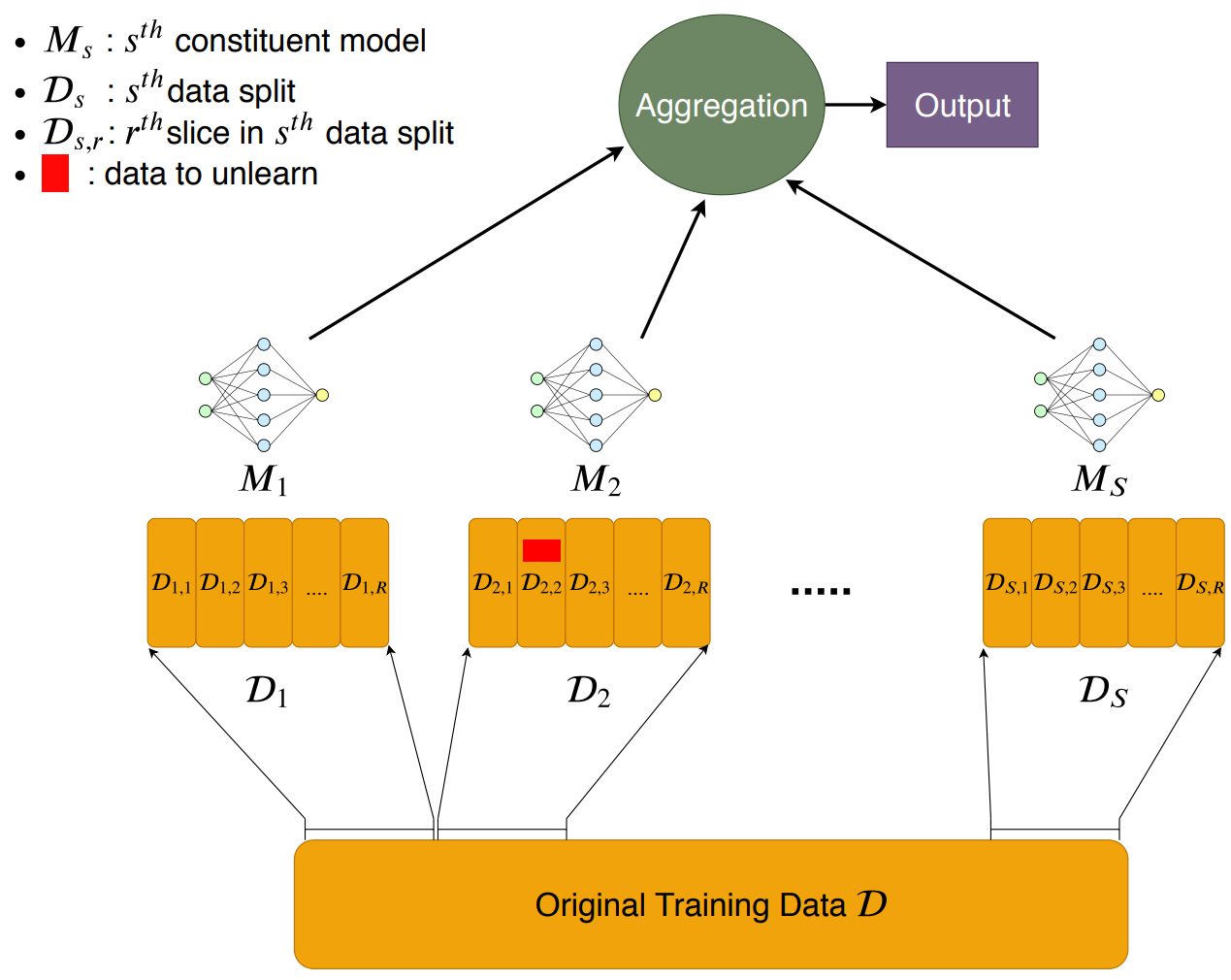
首先，分片，把总的训练数据集D切分成D1,D2,…,Ds等小的数据集，

其次，隔离，把D1,D2,…,Ds分别用M1, M2…Ms等不同神经网络隔离训练， 继续阅读模型”遗忘”的启迪：Machine Unlearning(Forgetting)，“主动遗忘”和“彻底遗忘”，长时记忆与短时记忆，多伦多大学向量学院，SISA

人类大脑可以在“现实”和“想象”之间自由切换，这种控制力一部分可能是“感知”驱动的，但是，另一部分是什么？ — David 9

显然未来几年的趋势是，神经网络拥护者(Hinton等人)不再满足于模拟“低级”感知了，当下有一堆类似“因果推理”，“长期计划”，“抽象想象”，“知识提炼和探索”等更高级的认知问题需要模拟！这种认知问题科学家们叫：“系统2″的认知（System 2 Processing）　。

与视觉皮层的“快速直觉”认知不同（如CNN），System 2的认知更“慢”，更“高层”，但是，如何达到这种认知，没有人明确地知道。当然Hinton等人把他们的赌注下在“人工感知”上，即，只要原始的感知一层层不断往上堆，机器也能感受到“因果推理”，“长期计划”等的合理性，进而采取行动。而另一些认知科学家不这么认为，毕竟，没有理论依据也很难让人相信，更高级的认知是从“一大片混沌”中诞生的。

这也就是为什么Yoshua Bengio和Gary Marcus的AI辩论也不会有什么实质性进展。Yoshua Bengio等神经网络拥护者更关心怎么把可以工作的智能系统建成，而Gary Marcus更关心人类认知的理论探讨。

David认为“感知”一定重要(人是感知丰富的动物)，但Hinton等人似乎遗漏了什么，我们稍后探讨。

先回到主题，接着上一篇，这次AAAI2020主题演讲上另两位(Yann Le Cunn和Yoshua Bengio)也带来了他们对更高级“感知”的假设和实现细节。

当然，他们都在试图解决System 2的更高级认知问题，Yann Le Cunn提了3个重要方向，

1. 自监督学习（self-supervised learning），这个David 在以前较详细讨论过，不赘述了。

2. 对比学习(Contrastive Learning)和隐变量基于能量模型(latent variable energy-based models):

对比学习的底层的目标和胶囊网络相似，即人类有一种天性是：我们在预测和行动前，早就在大脑中存了类似“缓存”的东西（心理期望），拿着

加入David9的星球群，获得通行密码 , 阅读全文