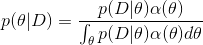如果人脑在执行任务时有特定模式,那么神经网络在增强学习中也应该有特定模式,而不是杂乱无章地更新 — David 9
我们在之前的文章中讨论过,Evolution Strategy和遗传算法等传统算法都可以在深度增强学习中发挥作用。其实,人们早就在神经网络中植入各种传统机器学习的方法(包括L2正则法等等)。
在2015年google的论文中就提到结合变分推断(variational inference)启发式更新神经网络的内部参数:
其性能效果堪比dropout方法,并且在增强学习中有较好表现。
那么,贝叶斯深度学习或者说变分推断(variational inference)如何应用在神经网络呢?
理论上,对于一般的深度神经网络,Loss如下:
![]() θ 是神经网络的内部参数集。xi, yi 即样本集中的一个样本。上式只是让训练损失最小。
θ 是神经网络的内部参数集。xi, yi 即样本集中的一个样本。上式只是让训练损失最小。
即,要找到一个最好的 θ* ,让 Ln(θ) 最小。
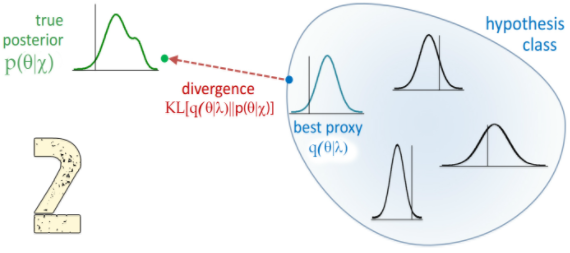
而在贝叶斯学派中,关心的是后验分布:
即,关心在数据D下模型参数θ 的分布。其中 α 是 ℝd 上的θ先验分布(可以理解为从α 中可以抽样得到 θ)。
而实际上,这一理想化的后验分布很难在实际中求解(我们很难穷尽神经网络所有可能的内部参数 θ)
实际中我们一般用一个替代分布q(θ|φ)去逼近后验分布p(θ|D), 如果无法知道α 的真正形式,我们就先造一个q(θ|φ)分布,使得变分自由能(variational free energy)最小:
David 9
Latest posts by David 9 (see all)
- 修订特征已经变得切实可行, “特征矫正工程”是否会成为潮流? - 27 3 月, 2024
- 量子计算系列#2 : 量子机器学习与量子深度学习补充资料,QML,QeML,QaML - 29 2 月, 2024
- “现象意识”#2:用白盒的视角研究意识和大脑,会是什么景象?微意识,主体感,超心智,意识中层理论 - 16 2 月, 2024