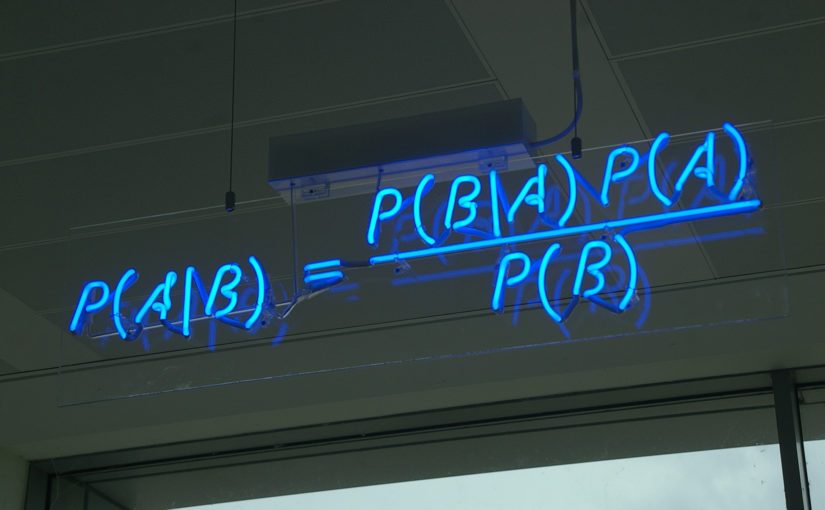这一期, 我们来谈一谈机器学习中的贝叶斯. 概率论中贝叶斯理论, 作为概率的一种“思考方式”, 十分通用. 当机器学习应用中, 贝叶斯的强大理论提现在多个领域, 包括超参数贝叶斯, 贝叶斯推断, 非参贝叶斯等等…
入门
机器学习中的贝叶斯, 首先要区分概率中频率学派和贝叶斯学派的. 网上有各种各样的解释, 其实, 我们可以从机器学习的角度去解释.
机器学习问题可以总结为: 找到一个好的 ![]() 代表一个模型,
代表一个模型, ![]() 表示这个模型的所有参数, 而这个模型就是我们能够训练出的最好模型(至少我们认为是最好的). 什么是最好的模型? 假设有未知数据集
表示这个模型的所有参数, 而这个模型就是我们能够训练出的最好模型(至少我们认为是最好的). 什么是最好的模型? 假设有未知数据集 ![]() , 如果
, 如果 ![]() , 那么这个模型就是最好的. 当然这是不可能的, 也许只有上帝才能对所有的未知100%准确预测. 但我们一定是希望
, 那么这个模型就是最好的. 当然这是不可能的, 也许只有上帝才能对所有的未知100%准确预测. 但我们一定是希望 ![]() 越大越好, 趋向于1.
越大越好, 趋向于1.
如何做到使得 ![]() 越大越好 ? 这就引出了概率论中的两大学派: 传说中的”频率学派”和”贝叶斯学派”. 两大学派区别在哪里? 看下面这个公式:
越大越好 ? 这就引出了概率论中的两大学派: 传说中的”频率学派”和”贝叶斯学派”. 两大学派区别在哪里? 看下面这个公式:
![]()
没错! 这就是大名鼎鼎的贝叶斯公式 ! 机器学习中, ![]() 是真实的训练数据或者抽样数据 .
是真实的训练数据或者抽样数据 . ![]() 是后验概率(posterior)分布 .
是后验概率(posterior)分布 . ![]() 是似然概率(likelihood).
是似然概率(likelihood). ![]() 是先验概率分布(prior).
是先验概率分布(prior). ![]() 是归一化”证据”(evidence)因子.
是归一化”证据”(evidence)因子.
“频率学派”认为, 后验概率和先验概率都是不存在的, 模型 ![]() 不论简单复杂, 参数已经是上帝固定好了的, 只要根据大数定理, 当训练数据足够大, 我们就能找到那个最好的
不论简单复杂, 参数已经是上帝固定好了的, 只要根据大数定理, 当训练数据足够大, 我们就能找到那个最好的 ![]() . 于是公式变为:
. 于是公式变为:
![]()
无论有没有 ![]() , 抽样数据
, 抽样数据![]() 出现的概率都是一样的, 因为任何数据都是从上帝指定的模型中生成的. 于是我们找到
出现的概率都是一样的, 因为任何数据都是从上帝指定的模型中生成的. 于是我们找到 ![]() 的任务就很简单, 最大化
的任务就很简单, 最大化 ![]() 似然概率就行了. 数据量越大, 模型拟合度越高, 我们越相信得到的
似然概率就行了. 数据量越大, 模型拟合度越高, 我们越相信得到的 ![]() 越接近上帝指定的那个
越接近上帝指定的那个 ![]() . 所以”频率学派”预测投硬币正反的概率的方法就是, 投10000次硬币吧, 看看正面出现多少次. 这种基于统计的预测有很多缺点, 首先它指定了一个固定概率, 如果上帝指定的模型不是固定的呢? 另外, 如果数据量不足够大, 预测会不会非常不准确? 当数据维数增大时, 实际计算量也会变得非常大.
. 所以”频率学派”预测投硬币正反的概率的方法就是, 投10000次硬币吧, 看看正面出现多少次. 这种基于统计的预测有很多缺点, 首先它指定了一个固定概率, 如果上帝指定的模型不是固定的呢? 另外, 如果数据量不足够大, 预测会不会非常不准确? 当数据维数增大时, 实际计算量也会变得非常大.
而“贝叶斯学派”认为, 人类的知识是有限的, 我们不知道上帝的安排, 就先假设一个先验(我们已有的知识), 再根据训练数据或抽样数据, 去找到后验分布, 就能知道模型最可能是个什么样子. 因此 ![]() 和
和 ![]() 都是存在的.
都是存在的. ![]() 是已有的我们认为
是已有的我们认为 ![]() 应该是什么样的分布. 请注意
应该是什么样的分布. 请注意![]() , 表示我们对模型也是抽象出一个分布的, 就是说, 模型不再是固定的, 如果有10个模型的候选, 我们认为一个模型的概率更大, 而另一个模型的概率更小而已. 所以, “贝叶斯学派”预测投硬币正反的概率的方法是, 分100组实验, 每次投100次硬币, 我们研究下, 正反面出现的比例作为随机变量, 到底这个随机变量更可能符合什么分布 ? (有可能是符合正态分布均值在0.5吗?) . 再举个例子, Beta分布就是伯努利分布的共轭先验分布. 即, 伯努利分布的参数是Beta分布中的随机变量, 因此, Beta分布可以生成伯努利分布, Beta分布又称分布之上的分布. 具体可参见文章如何理解Beta分布和Dirichlet分布? 理解了一个分布可以生成另一个分布, 多层次贝叶斯模型就更容易理解了, 简要地说就是, 选择不同的先验去训练预测模型, 得到的模型有优劣之分. 具体可参加这篇文章: “A/B Testing with Hierarchical Models in Python” .
, 表示我们对模型也是抽象出一个分布的, 就是说, 模型不再是固定的, 如果有10个模型的候选, 我们认为一个模型的概率更大, 而另一个模型的概率更小而已. 所以, “贝叶斯学派”预测投硬币正反的概率的方法是, 分100组实验, 每次投100次硬币, 我们研究下, 正反面出现的比例作为随机变量, 到底这个随机变量更可能符合什么分布 ? (有可能是符合正态分布均值在0.5吗?) . 再举个例子, Beta分布就是伯努利分布的共轭先验分布. 即, 伯努利分布的参数是Beta分布中的随机变量, 因此, Beta分布可以生成伯努利分布, Beta分布又称分布之上的分布. 具体可参见文章如何理解Beta分布和Dirichlet分布? 理解了一个分布可以生成另一个分布, 多层次贝叶斯模型就更容易理解了, 简要地说就是, 选择不同的先验去训练预测模型, 得到的模型有优劣之分. 具体可参加这篇文章: “A/B Testing with Hierarchical Models in Python” .
现在可以总结, “频率学派”假设模型是固定的, 用大量数据去计算最大似然估计, 就能获得好的预测模型. “贝叶斯学派”假设模型是非固定的, 模型参数本身也服从一个分布![]() , 重点关心的是计算出后验概率不断调整这个分布, 找到最大概率的那个
, 重点关心的是计算出后验概率不断调整这个分布, 找到最大概率的那个![]() . 找到上帝更可能选用的那个模型. 即:
. 找到上帝更可能选用的那个模型. 即:
![]()
两个思想的比较就到这里, 我想, 孰优孰劣, 大家心里一定已经有了答案.
Bayesian思想 笔记
1. 贝叶斯是关注后验概率的. 而不是最大似然.
2. 期望的计算 函数的期望, 只要对函数![]() 给到一个
给到一个![]() 概率分布:
概率分布:
![]()
3. 方差 ![]()
4. 如果 ![]() , 则:
, 则: ![]()
5. (1) True Positive: 模型认为是对的, 确实是对的概率.
(2) False Positive: 模型认为是对的, 结果是错的概率.
(3) True Negative: 模型认为是错的, 确实是错的概率.
(4) False Negative: 模型认为是错的, 结果是对的概率.
 Loading...
Loading...
David 9
Latest posts by David 9 (see all)
- 修订特征已经变得切实可行, “特征矫正工程”是否会成为潮流? - 27 3 月, 2024
- 量子计算系列#2 : 量子机器学习与量子深度学习补充资料,QML,QeML,QaML - 29 2 月, 2024
- “现象意识”#2:用白盒的视角研究意识和大脑,会是什么景象?微意识,主体感,超心智,意识中层理论 - 16 2 月, 2024