卡内基梅隆大学（CMU），那些经受住时间考验的机器学习论文–第二弹：动态主题模型

这一弹，接着上一期，这次，我们要解释一种典型的机器学习算法——动态主题模型（Dynamic Topic Model）。

概率主题模型和概率图模型是每个做文本挖掘的学者的必学课题。其中最常见的主题模型是隐含狄利克雷分布（LDA）。当然，本文的动态主题模型也是主题模型的一种，不过为了方便理解，我们还是来回顾一下LDA。

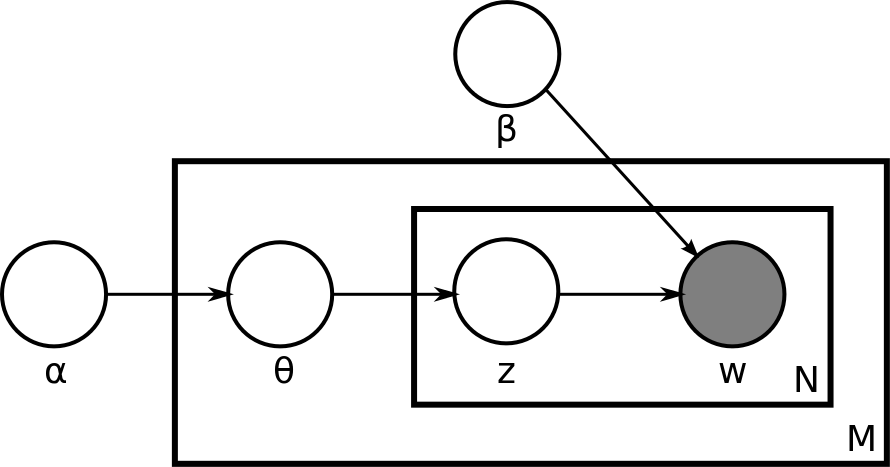
我们定义：

α 是狄利克雷先验的参数，是每个文档可能的主题分布。

，当α 落实到一个文档m，是文档m的主题模型。而且α代表的是狄利克雷分布，代表的是多项式分布。 α很明显是的共轭先验。

β 是狄利克雷先验的参数，但是，它是每个主题可能的文字分布。

 是在文档m中，第n个文字的主题。

 是那个真正生成出来的文字，文档m中的第n个文字。

这就是很传统的LDA概率生成模型。关键是训练好每个文档可能的主题分布，以及每个主题可能的文字分布，这两组关键的超参数。

但是！LDA有一个很大的前提假设，就是：所有的训练文档都是没有前后顺序的。这个假设其实是不切实际的，因为随着时间推移，同样主题的文档也可能会有不同的文字表达。比如以前我们叫年轻的帅哥是“小帅哥”，而，现在很多人表达为“小鲜肉”。如果我们把时间序列的因素考虑到文档的前后排列，然后进行训练，就会需要动态主题模型。

即，随着时间的推移，主题模型的参数应该是不同的，每个文档可能的主题分布会随着时间改变，每个主题可能的文字分布也会随着时间改变：

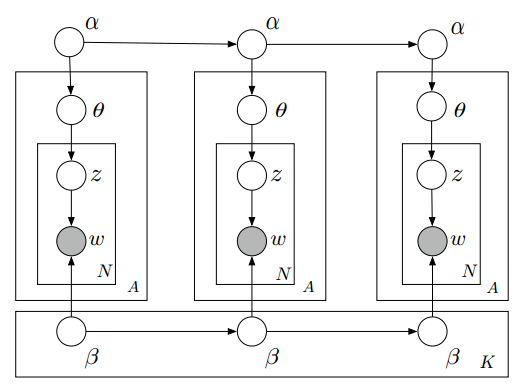
假设我们把训练的文档集合分成三个部分，分别是，2014年的文档集，2015年的文档集，2016年的文档集。这样就应该有三个主题模型，因为，每个年份都有不同的主旋律和各自独特的文字表述方式，不是吗？

我们定义：

 是在时间t 的每个文档可能的主题分布。

 是在时间t 时，主题k可能的文字分布。

 是在时间t 时文档t 的可能的主题分布。

 是在时间t 时，在文档d中第n个文字的可能主题。

 就是t时间的生成文字。

可以看到，这里的定义中，只是加了时间特征而已。

因此，围绕时间t这个时间段的生成过程，可以概括为如下：

1. 从上一个时间段t-1，生成这个时间段t 的狄利克雷分布，表示主题k可能的文字分布：
     注意，这里的N代表高斯分布，均值为上一个时间段的狄利克雷分布，方差要训练得到，这种假设很符合直觉，每一个相邻的时间段里，文档和主题的分布变化不会太大。
2. 同样地，从上一个时间段t-1生成这个时间段t 的狄利克雷分布：
3. 为每一个文档:
   1. 生成主题分布：
          不是很明白为什么这里也是高斯分布，似乎直接可以从生成多项式分布啊？
   2. 为每个文字:
      1. 生成主题：
      2. 生成文字 : 

注意这里 是把高斯分布的参数, 隐射到多项式分布标准化后的参数 :.

以上就是动态主题模型最简单的文档生成过程. 至于如何做后验推演(Approximate Inference), 变分卡尔曼滤波(Variational Kalman Filtering), 变分小波回归(Variational Wavelet Regression) , 请阅读原论文.

说道时间序列, 这里给一张变分卡尔曼滤波和变分小波回归的对比图:

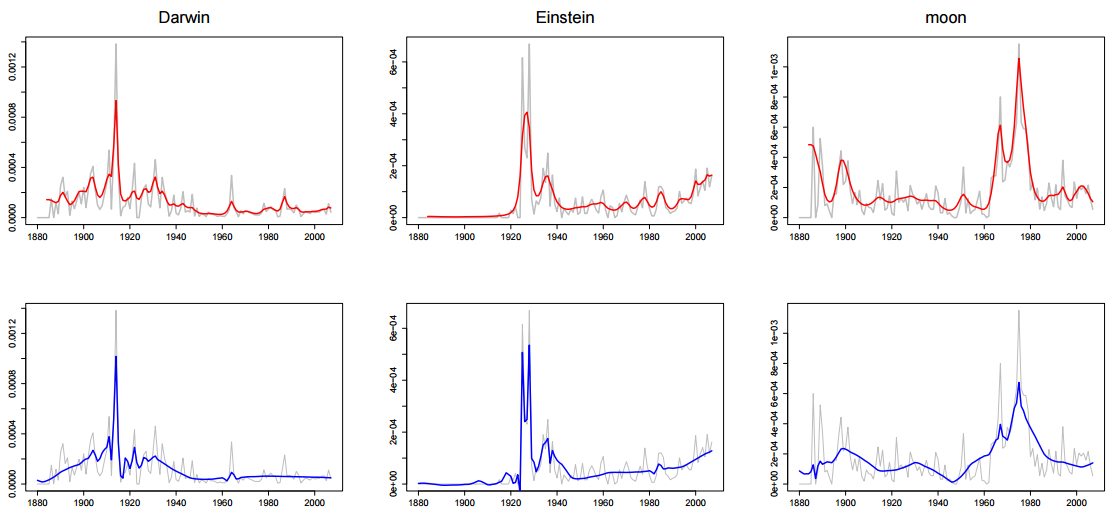
上面一行是变分卡尔曼滤波训练出的模型(红色)对出现”Darwin”, “Einstein”, “moon”的时间序列判断, 下面一行是变分小波回归训练出的模型(蓝色)对出现”Darwin”, “Einstein”, “moon”的时间序列判断. 可以看出, 用变分小波回归训练的出的动态主题模型对于瞬时激增的峰值预测相当准确(Einstein在1925年左右有一个激增). 当然, 这正是小波预测的优势在所在.

 

参考文献：

1. Dynamic Topic Models
2. 卡耐基梅隆大学机器学习专业 历年最佳论文
3. 什么叫共轭先验或者共轭分布？

本文章属于“David 9的博客”原创，如需转载，请联系微信yanchao727727，或邮箱：yanchao727@gmail.com